Objektu bat indar baten eraginpean higitzen denean gertatzen den energia-transferentziaren neurria da; lana egin dezan, higiduraren norabidean zuzenduriko osagairen bat izan behar du indarrak. Lana magnitude eskalarra da, energia bera den moduan. Lanaren unitateak ere energiaren unitate berberak dira: joule (J), Nazioarteko Unitate Sisteman ari bagara.

Lana nola kalkulatu

Kalkulua egiteko, kasurik errazenean, objektua, indar konstante baten eraginpean, lerro zuzen batean barrena higitu behar da. Hona hemen lana (W) lortzeko bidea:

$W=\mathit{F}\cdot \mathit{d}=\mathit{F}\cdot \mathit{d}\text{cos }\theta$

F eta d, hurrenez hurren, indarra eta desplazamendua dira (biak bektoreak), eta haien arteko biderketa eskalarra egin behar dugu lana lortzeko; hori dela eta, adierazpeneko θ angelua F eta d bektoreen artekoa da.

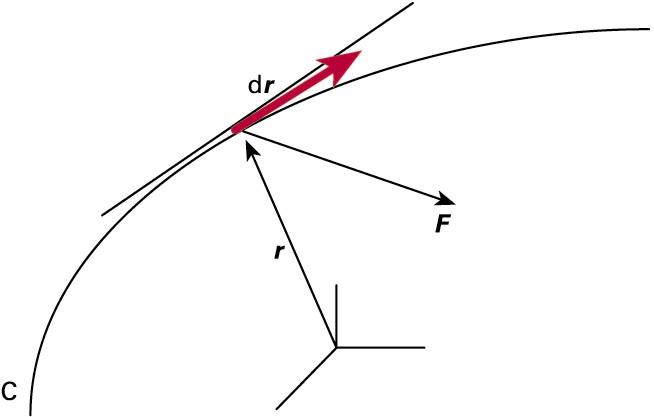
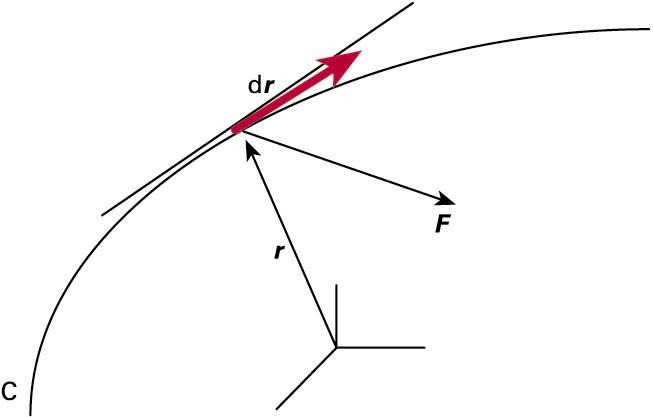
Gehienetan, ordea, gorputzaren higidura ez da zuzena izango edo indarra konstante, eta, horrenbestez, ezingo dugu aurreko adierazpena erabili. Irtenbidea gorputzak espazioko bi punturen artean egindako ibilbidea hainbat tarte txikitan banantzean datza; hala, indarra konstantetzat jo ahal izango dugu tarte “zuzen” txiki bakoitzean, eta, azkenean, tarte horietako guztietako lanak batuz lortuko dugu indarrak espazioko bi puntuen artean guztira egindako lana. Hizkera matematikoaz baliatuz, honelako lerro-integral baten bitartez egin dezakegu hori:

$W=\underset{C}{\int }\mathit{F}\cdot d\mathit{r}$

F eta r, hurrenez hurren, indarra eta posizio-bektorea dira, eta C ikurrak gorputzaren ibilbidea adierazten du (integrala ibilbide horretan barrena egin behar da, ibilbideko hasierako puntutik bukaerakora).

Lanaren kalkulua integralaren bidez

Eman ditugun lanaren bi adierazpenak aintzat hartuz, berehala konturatuko gara indar ez-nuluek lan nulua egin dezaketela zenbait egoeratan. Batetik, objektuaren desplazamendurik ez badago, ez dago lanik: zutik gaudela pisu mardul bati eusten badiogu, ez dugu lanik egingo (ez diogu objektuari energiarik transferituko), ez baitago higidurarik. Bestetik, indarra eta desplazamendua elkarzutak direnean, ez da lanik egiten gorputzaren gainean. Demagun soka baten mutur batean harri bat lotu, eta, beste muturrari eskutik helduta, abiadura konstantean birarazi dugula gure buru gainean. Hor ere ez dago energia-transferentziarik (harriaren abiadura eta altuera ez dira aldatu), eta, ondorioz, ez dago lanik. Adierazpen matematikoak garbi uzten digu hori, bi bektore elkarzuten arteko biderkadura eskalarra zero baita.

Lana eta energia

Gorputz baten gainean lana (W) egiten dugunean, haren energia zinetikoa (Ek) aldatzen dugu. Lanaren eta energiaren teoremak lotzen dizkigu bi magnitudeok, gorputza ibilbideko 1 puntutik 2 puntura higitu denean:

$W={\Delta E}_k=E_{k\mathrm{,2}}-E_{k\mathrm{,1}}=\frac{1}{2}{mv}_2^2-\frac{1}{2}{mv}_1^2$

non m den gorputzaren masa, eta v, berriz, abiadura. Konturatu gaitezen lana negatiboa ere izan daitekeela (indarra eta desplazamendua aurkako bektoreak direnean), eta, halakoetan, gorputzaren energia zinetikoa murriztu egingo da. Gainera, egoera arruntenetan ageri ohi diren indar gehienak kontserbatzaile deritzon motakoak dira; alegia, halako indarrek gorputz baten gainean lana egiten dutenean, lan hori berreskuragarria izaten da. Lana “metatu” egiten da, eta beste energia-mota bat dela pentsa dezakegu; energia horri energia potentzial esaten diogu. Halakoak dira, besteak beste, grabitazio-indarra, malgukiarena eta indar elektrostatikoa. Marruskadura, ordea, ez da kontserbatzailea. Indar kontserbatzaileekin ari garenean, indarrak egindako lana (W) dagokion energia potentzialaren (Ep) bidez lor daiteke:

$W=-{\Delta E}_p=-(E_{p\mathrm{,2}}-E_{p\mathrm{,1}})$

Ondorio garrantzitsu bat atera daiteke eman berri dugun adierazpenetik. Izan ere, lanaren eta energiaren teoremara eramaten badugu, ekuazio hau idatzi ahal izango dugu:

$-\Delta U={\Delta E}_k$ edo $E_{p\mathrm{,1}}-E_{p\mathrm{,2}}=E_{k\mathrm{,2}}-E_{k\mathrm{,1}}$ edo $E_{k\mathrm{,1}}+E_{p\mathrm{,1}}=E_{k\mathrm{,2}}+E_{p\mathrm{,2}}$ edo $(E{}_k+E_p{)}_1=(E_k+E_p{)}_2$

Energia zinetikoaren eta potentzialaren baturari energia mekaniko deritzo, eta, azken emaitza horren arabera, gorputza indar kontserbatzaileen eraginpean dagoenean haren energia mekanikoak konstante dirau.

Lana termodinamikan

Orain arte esandako guztia indarrek egindako lan mekanikoari dagokio, baina lanaren kontzeptua termodinamikara ere zabaldu daiteke; esate baterako, ontzi batean dagoen gas bat konprimitzen badugu, gasaren gainean lan termodinamikoa egin dela esango dugu (indarra dago, bai eta desplazamendua ere; hortaz, lana egingo da). Gorago eman ditugun lana kalkulatzeko adierazpenak moldatu egin behar dira termodinamikan erabili ahal izateko (termodinamika).