datu-analisi
- 1. Estat.
- sin. datu-azterketa
Datuen deskribapen murriztua eta informazioduna lantzeko prozesua.
1. Estat.
-

Zenbait maiztasun-banaketa -
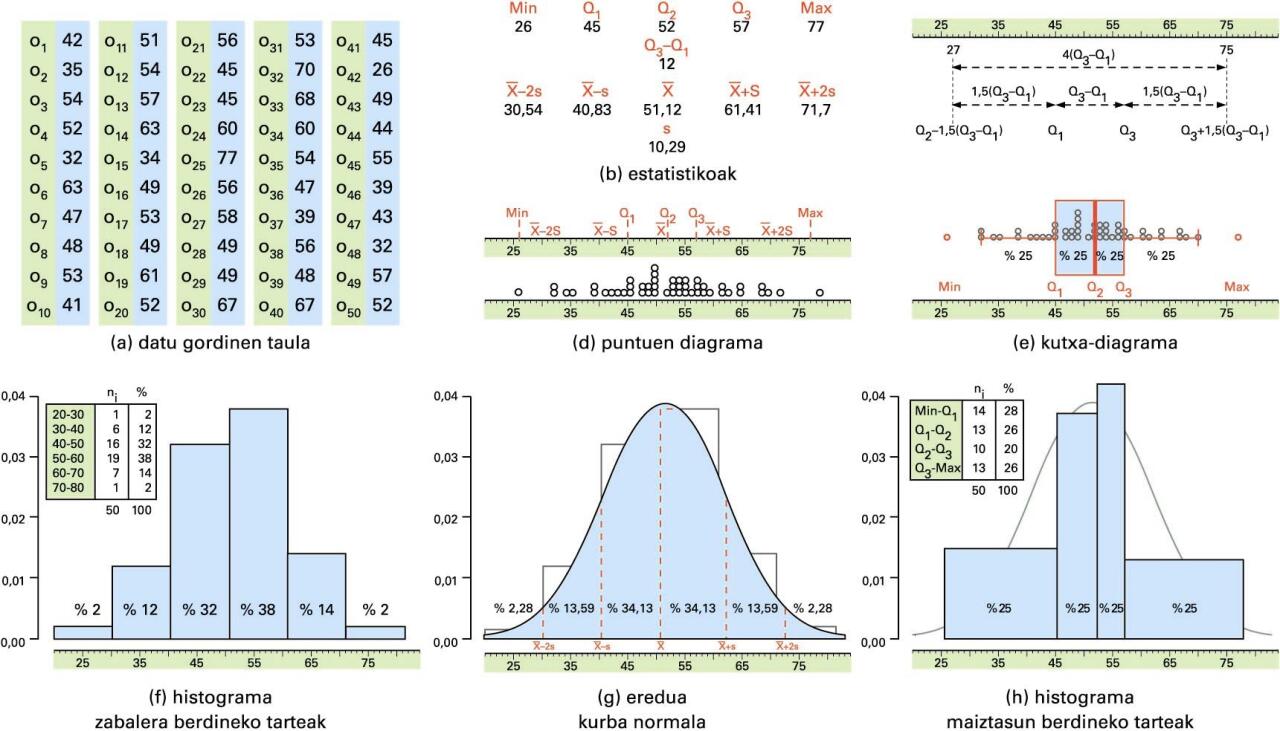
Aldagai kuantitatibo baten azterketa estatistikoa -
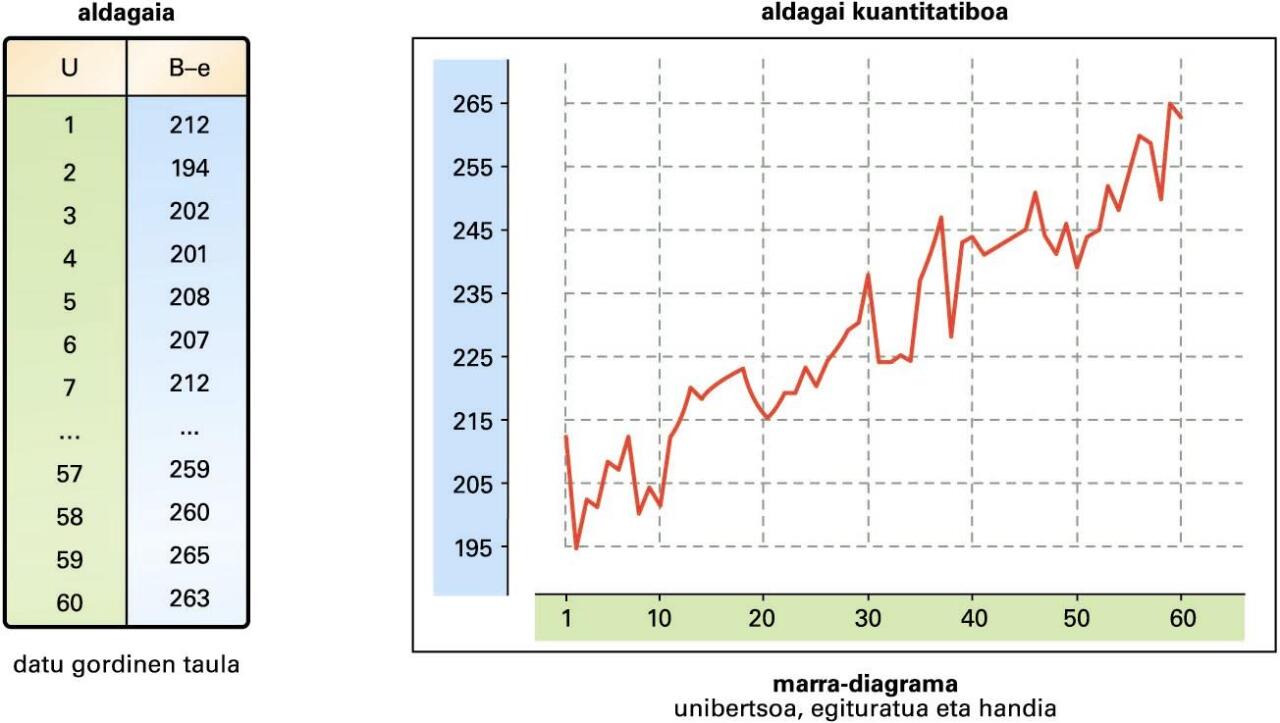
Aldagai kuantitatiboa: denbora-segida -
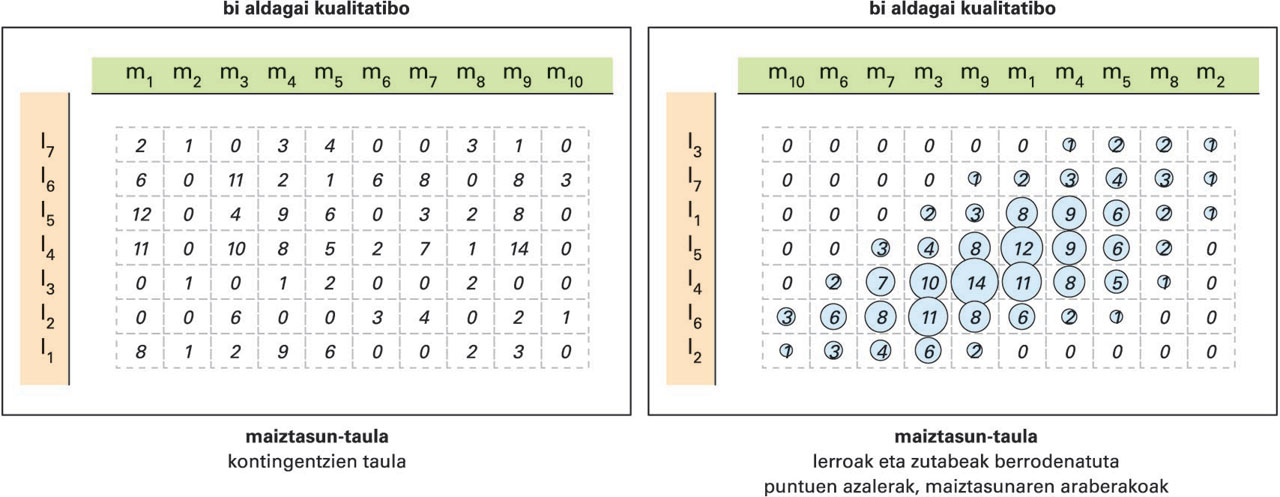
Bi aldagairen arteko lotura: biak kuantitatiboak -
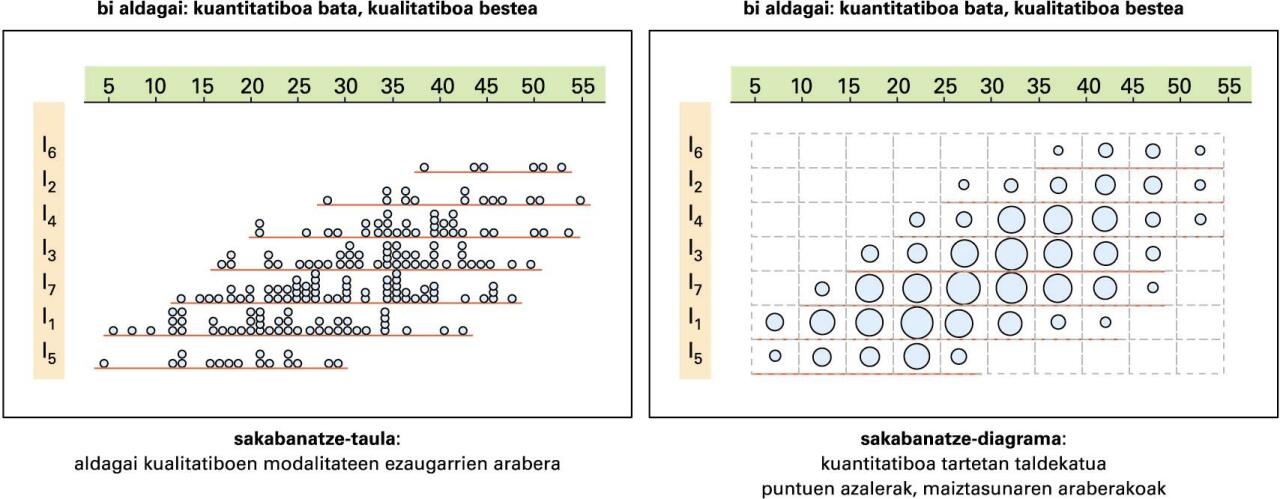
Bi aldagairen arteko lotura: bata kuantitatiboa eta bestea kualitatiboa -
Bi dimentsioko eredu normala bi aldagai kuantitatiboren arteko loturari egokitzea -
Eredu normala: histograma eta bi dimentsioko kurba normala
- 1. Estat.
- Datuen deskribapen murriztua eta informazioduna lantzeko prozesua.
Datu-analisia Edit
Egilea: Yosu Yurramendi
Datuak bildu eta aztertzeari ekin baino lehen, ia beti dago horretara bultzatzen duen arrazoiren bat, usteren bat atzean. Zaila da uste izatea aldez aurretik ez dagoela ezer bilatzerik. Dena dela, jo dezagun datu-multzo hutsa besterik ez dugula esku artean, eta hor miatu beharra daukagula informazioa erauzi eta mamitzearren.
Estatistika deskribatzailea da horretaz arduratzen den metodo eta tresnen arloa (estatistika). Arlo horri datu-analisi miatzaile ere esaten zaio (EDA, exploratory data analysis) —antza, hipotesiak baieztatzeko edo ezeztatzeko datu-analisitik bereizteko (CDA, confirmatory data analysis)—, baita datu-analisi besterik gabe ere. Konputazioaren ikuspegitik, data mining ("datu-meatzaritza") da gaur egun maiz erabiltzen den eta arlo honi dagokion termino bat.
Errealitateko problema bat aztertzerakoan, erlazio-sistema bat definitzen da, eta horren euskarri nagusiak unibertsoa eta behaketa-espazioak dira. Datu-analisiaren bitartez, datuen deskribapen murriztu eta informazioduna azaldu nahi da; hau da, unibertsoko objektuen arteko erlazio berri eta garrantzitsuak, behaketa-espazioetako modalitateen artekoak, baita objektuen eta modalitateen artekoak bistaratzea eta hierarkizatzea ere.
Unibertsoaren eta behaketa-espazio bakoitzaren arteko egokitzeari aldagai deritzo. Funtsean, bi motatako aldagaiak bereizten dira: kualitatiboak eta kuantitatiboak. Lehenengo motakoaren behaketa-espazioak kualitate bat adierazten du. Bigarren motakoaren behaketa-espazioa, aldiz, zenbakiena da; hau da, zenbakietan eta haien propietateetan oinarritzen da.
Datu-analisiaren teknikak unibertsoaren egituraren, aldagai-kopuruaren eta aldagai-motaren arabera sailkatzen dira. Teknika horien oinarria aldagai bakar baten analisia da; gero, bi aldagairen arteko erlazioaren analisia egiten da, eta haien gainean eraikitzen dira aldagai anitzeko analisiak.
Taulak, grafikoak, zenbakizko adierazle edo estatistikoak, eta datuei egokitzen zaizkien ereduak izaten dira erabiltzen diren tresnak. Batzuetan, hobeto ulertzearren, datuen eraldaketa edo transformazioak egitea ere komeni izaten da.
ALDAGAI BAKAR BATEN ANALISIA
Datu-analisirako dauden metodo eta tresna sinple edo bakunenak aldagai bakar bati dagozkionak dira.
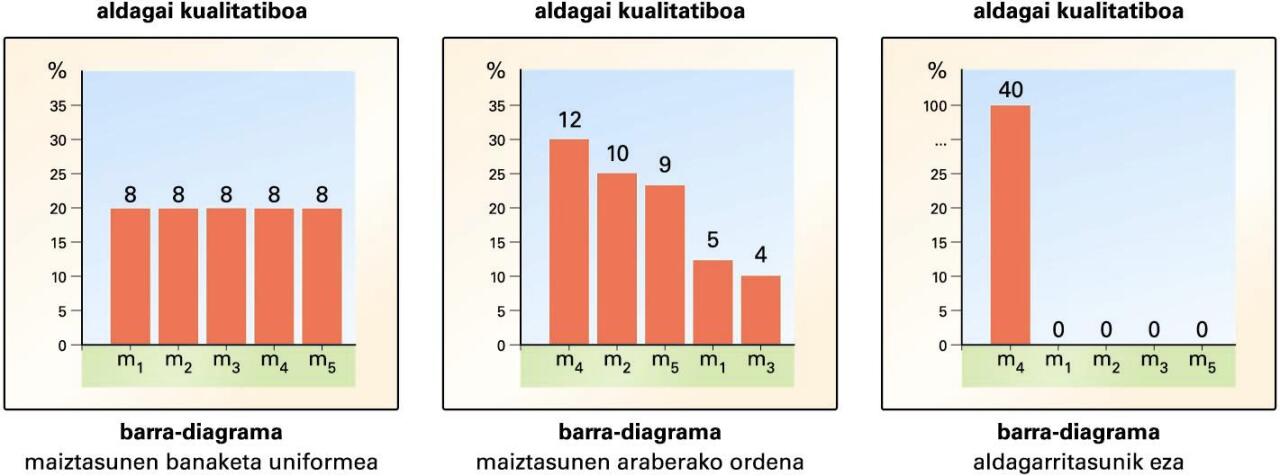
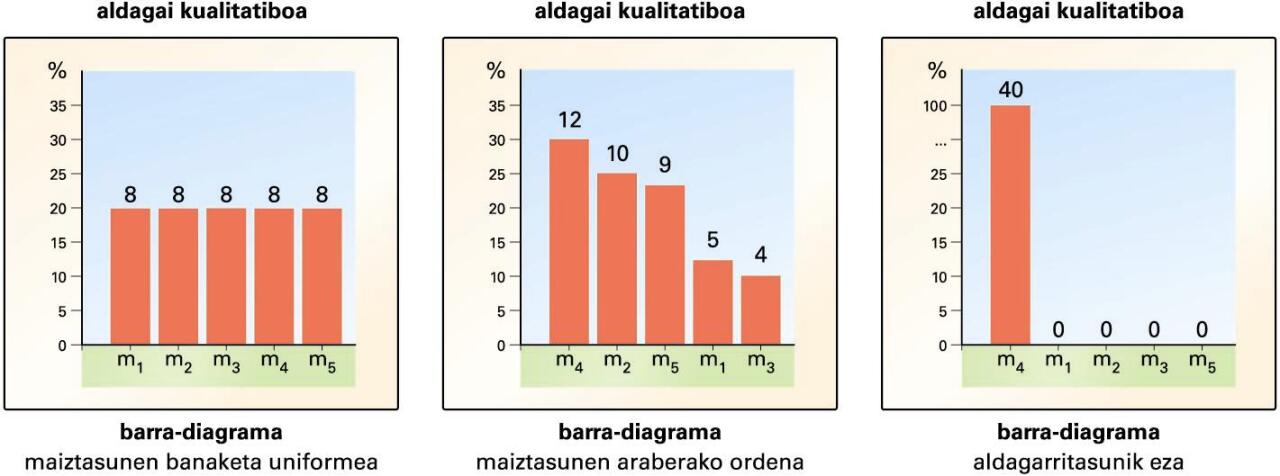
Hurrengo irudian ageri da, adibidez, egiturarik gabeko unibertso bati behatu zaion aldagai kualitatibo baten azterketa grafikoa zenbait kasutan.
Moda esaten zaio maizen gertatu den modalitateari; horrek adierazten du zein izan den “irabazlea” modalitateen artean. Modalitate bakar bat aipatzekotan, huraxe aipatuko genuke. Aldagarritasuna neurtzeko tresnak ere badaude, eta, agian, ezagunena edo erabiliena informazio-teorian oinarritzen den entropia da. Aldagarritasunik ez dagoenean, 0 balioa du; aldagarritasunik handiena dagoenean (maiztasunen banaketa uniformea denean), berriz, log2p, p izanik aldagaiaren modalitate-kopurua. Gainerako kasuetan, bi mutur horien artean kokatzen da entropiaren balioa.
Zenbait maiztasun-banaketa
Aldagai kuantitatiboari dagokionez, ordea, behaketa-espazioaren egitura aberatsagoa denez, azterketa sakonago bat egin daiteke.
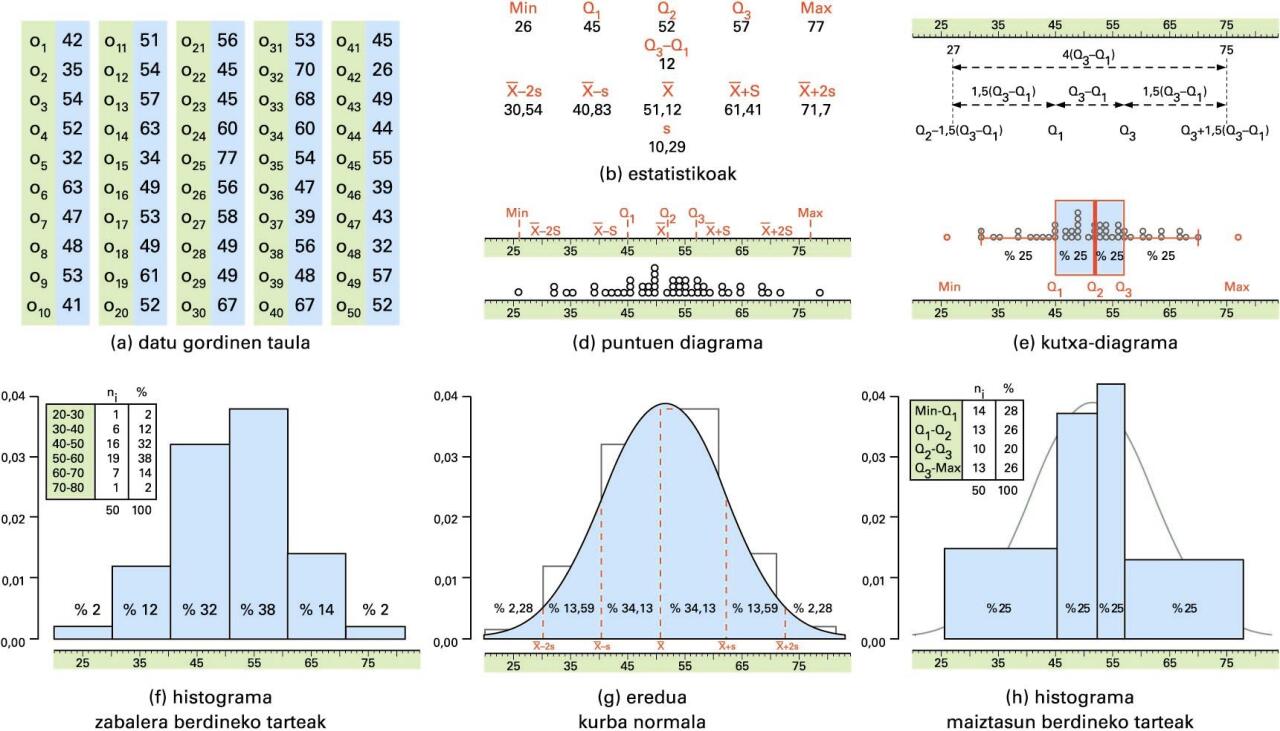
Datu-multzo jakin bat izanda, oinarrizko zenbait estatistiko edo zenbaki-multzoaren adierazle kalkula daitezke. Ezagunenak hauek dira: zenbakien ordenan oinarritutakoak (minimoa eta maximoa, mediana (Q2) eta kuartilak (Q1 eta Q3)) eta zenbakien propietateez baliatuz kalkulatutakoak (kuartilen arteko ibilbidea IQR = Q3- Q1, batezbestekoa (), desbideratze estandarra (s), eta beste ( - s, + s). Horietako batzuek datuen erdialderako joera azaltzen dute (mediana eta batezbestekoa), eta beste batzuek datuen sakabanatze-neurria (kuartilen arteko ibilbidea, desbideratze estandarra). Halako balio gutxi batzuk ezagututa, ez da zaila izaten buruz irudikatzea gutxi gorabehera nolakoa izan den aldagaiaren banaketa.
Irudikatze hori zuzenagoa da grafikoki azaltzen bada. Oinarritzat hartuta unibertsoko objektuen balioen kokapena zenbaki errealen ardatzean, ordenan oinarritutako estatistikoen bitartez kutxa-diagrama osatzen da, eta haien bitartez salatu edo erabaki daitezke zein diren objektu bitxiak (outliers).
Aldagai kuantitatibo baten azterketa estatistikoa
Izan ere, zenbaki-zerrendetako zenbaki bitxi edo arraroak datuak biltzean egindako akatsengatik edo objektu bitxiengatik gertatzen dira. Arreta berezia behar dute horiek, baztertuak izan ala leku berezi bat eman, txosten estatistikoan emaitzetan eragin nabarmenegirik izan ez dezaten.
Gerta liteke, orobat, datu-multzoan bi azpimultzo edo gehiago bereiztea. Kasu horretan, merezi izaten du bakoitza bere aldetik aztertzea, emaitzak ez desitxuratzearren.
Datuak tartetan taldekatuz gero, aldagaiaren banaketa mamituak osa daitezke. Irudian, bi modu agertzen dira: bata zabalera berdineko tarteak osatuz, eta bestea maiztasun berdineko tarteak osatuz. Halako bakoitzari histograma bat dagokio; jarraitutasuna adierazten duen barra-diagramaren antzekoa da, eta tarte bakoitzaren gainean eraikitzen den laukizuzenaren azalerak maiztasuna adierazten du.
Irudiaren arabera, datuei egokitu dakieke aldez aurretik definituta dagoen eredu bat. Irudian, hain ezaguna den eta kanpaiaren itxura duen kurba normala egokia dela ematen du, tarteei egokitzen dizkien maiztasunak, maiztasun-banaketak, berdintsuak baitira. Eredu bat egokitzean, aldagaiaren banaketa erabat mamitua geratzen da eredu horren formula matematikoan, eta halako formula batek dituen bi parametroen balioetan: batezbestekoa eta desbideratze estandarra.
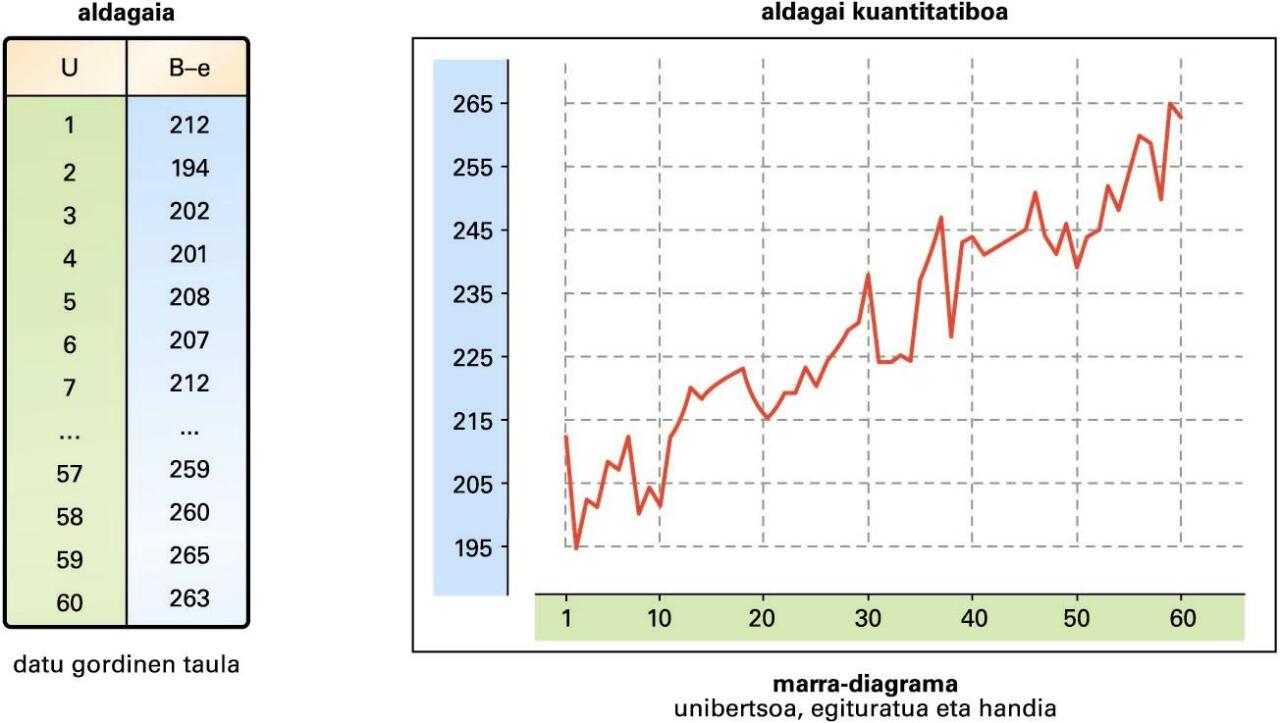
Unibertsoa egituratua dagoenean, aldez aurretiko informazioa handiagoa denez, halako kalkulu eta formulak ez dira nahikoak, horietan ez baitira kontuan hartzen objektuen arteko erlazioak. Hurrengo irudian, unibertsoaren egitura zenbaki errealena bera duen aldagai kuantitatibo baten analisi grafikoa ageri da (denborarena kasu). Halako datuei luzeratarako datu esaten zaie. Horien azterketak bestelako teknikak eskatzen ditu, betiere aurrekoetan oinarrituta.
Aldagai kuantitatiboa: denbora-segida
Unibertsoaren egitura aberatsagoa den heinean, teknikak bereziagoak izaten dira. Unibertsoaren egitura espaziozkoa (mapak, irudiak, grafoak) izan daiteke, baita espazio-denborazkoa ere.
Bi aldagairen arteko erlazioaren analisia
Bi aldagairen arteko erlazioa aztertzeko, kontuan hartu behar da zer motatako aldagaiak diren: biak kualitatiboak, biak kuantitatiboak, ala bata kualitatiboa eta bestea kuantitatiboa. Aztertzeko oinarria aldagai bakar batekin erabiltzen diren tresnek osatzen dute, baina kasu bakoitzean berezko grafikoak eta berezko adierazle edo erlazio-neurriak erabiltzen dira.
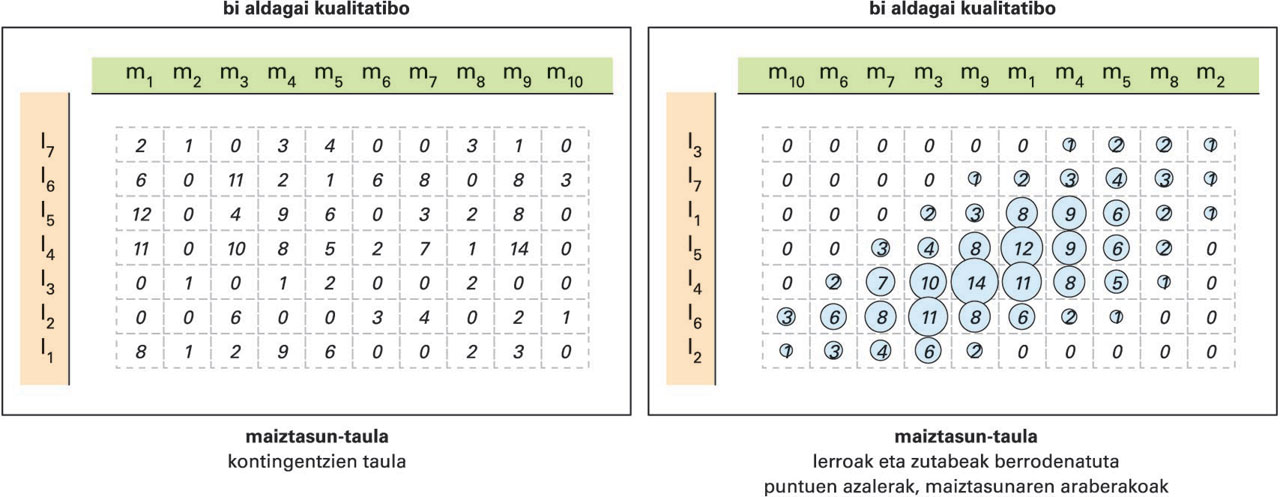
Bi aldagaiak kualitatiboak direnean, bi behaketa-espazioen modalitateak gurutzatzen dituen oinarrizko maiztasun-taula besterik ez dago erlazioa aztertzeko, kontingentzia-taula deritzona. Datu-analisiaren teknikak modalitateak taldekatzeko (clustering edo mordokako analisia) eta berrordenatzeko (faktore-analisia) balio izaten dute, erlazioa, izatekotan, nabarmenago gera dadin.
Erlazioaren indarra neurtzeko, estatistiko bat baino gehiago erabiltzen da, baina ezagunenak khi karratua eta informazio-teoriaren entropian oinarritutako elkarrekiko informazioa dira. Azken finean, biek neurtzen dute elkarren arteko ereduzko independentziaren egoeratik zein urrun kokatzen den (distantzia moduko formulatzat har daiteke) bien arteko erlazioa. Datuek baldintza matematiko jakin batzuk betez gero, bi neurriek gauza bera neurtzen dutela frogatuta dago.
Bi aldagairen arteko lotura: biak kuantitatiboak
Unibertsoak egiturarik izan gabe aldagai bat kualitatiboa denean eta bestea kuantitatiboa, datu-analisiko teknikak azken horren egituraz baliatzen dira bien arteko erlazioa azaltzen saiatzeko.
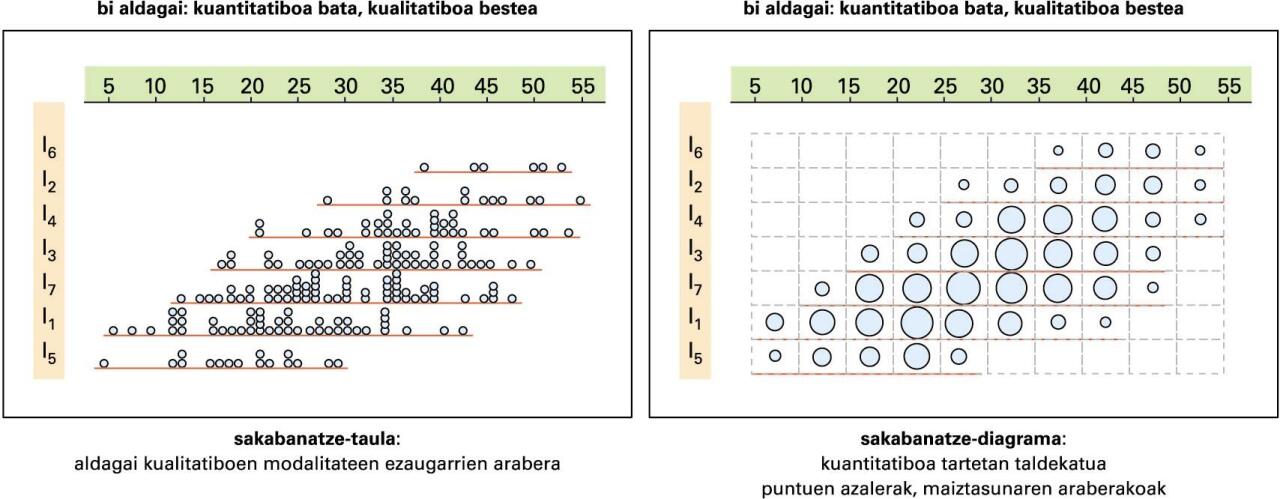
Bi aldagairen arteko lotura: bata kuantitatiboa eta bestea kualitatiboa
Modalitate bakoitzaren sakabanatze-diagrama kutxa-diagrama batez edo histograma batez ere adieraz liteke, batik bat, unibertsoaren tamaina handia denean.
Estatistiko ezagun gutxi dago halako bi aldagairen arteko erlazioaren indarra balio batean laburtzeko. Ezagunena eta karratua da, eta gainerakoak horren ondorengoak dira. Estatistiko hori aldagai kuantitatiboaren bariantza osoaren (total) deskonposizioetan oinarritzen da. Batetik, aldagai kualitatiboaren modalitate bakoitzaren barruko bariantzen batura kalkulatzen da (within), eta, bestetik, modalitateen arteko bariantza (between), modalitate bakoitzaren baliotzat batez besteko balio partikularra hartuta. Bariantza osoa beste bi horien batura denez (total = within + between), proportzio baten bitartez neur daiteke modalitateen zerikusia kuantitatiboaren aldagarritasunean (eta karratua = between/total). Modalitateen batezbestekoak berdinak balira (between = 0), ez legoke erlaziorik bi aldagaien artean (eta karratua = 0); oso desberdinak balira, aldiz, bai. Muturreko kasu hau da (eta karratua = 1) modalitate bakoitzaren banaketa hutsala denekoa, balio guztiak berdinak direnekoa, aldagarritasunik ez dagoenekoa alegia (bariantza partikularrak zero balio dutenekoa, eta, beraz, within = 0).
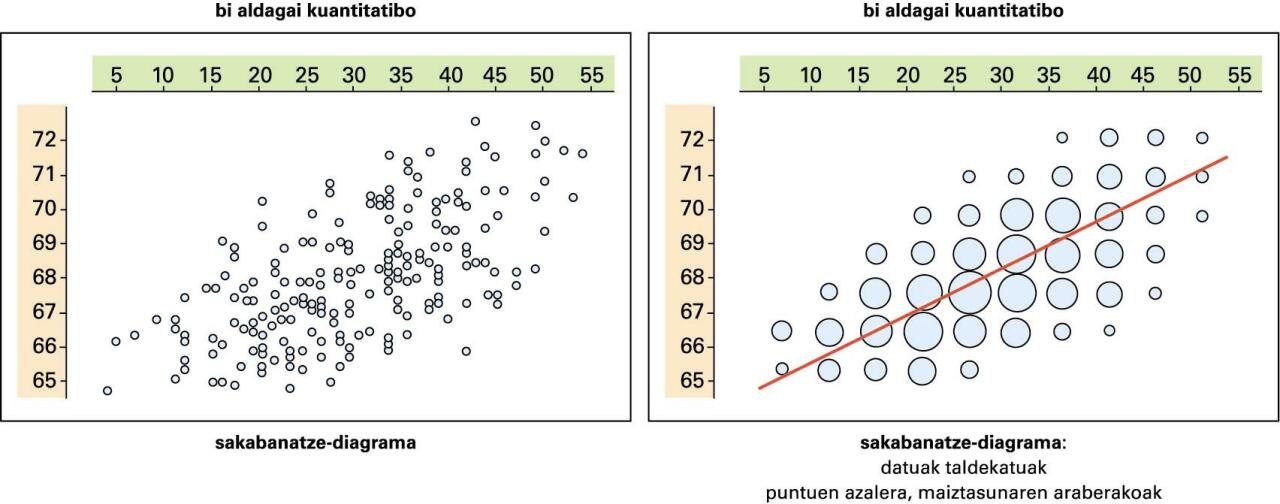
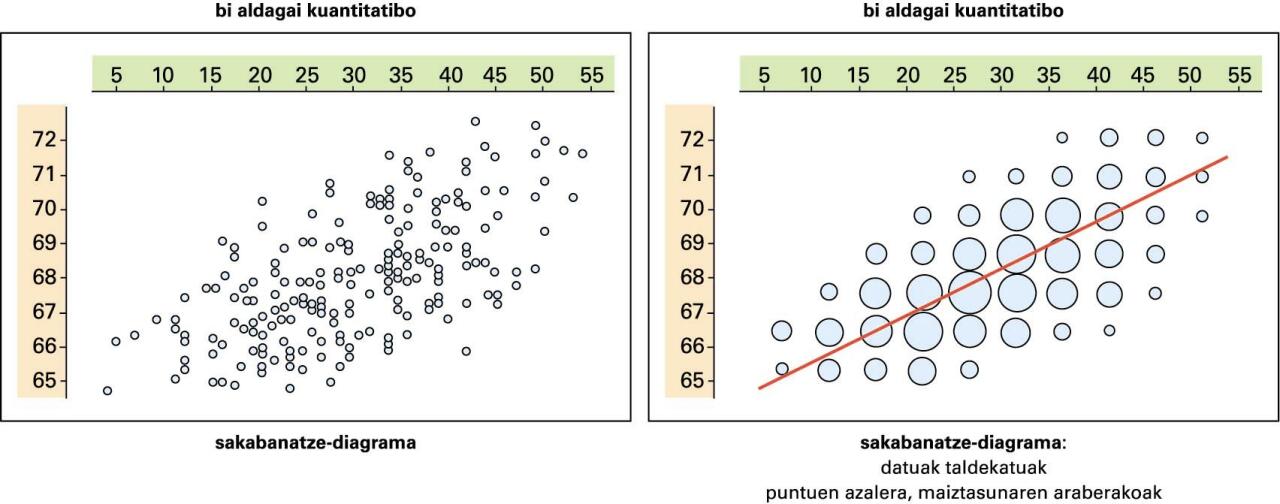
Bi aldagaiak kuantitatiboak direnean, bi dimentsioko sakabanatze-diagrama eraiki daiteke. Diagrama horretan ikus daiteke bi aldagaien artean erlaziorik ba ote dagoen, eta, izatekotan, nolakoa den hori.
Bi dimentsioko eredu normala bi aldagai kuantitatiboren arteko loturari egokitzea
Irudiari bi aldagaien arteko erlazio lineal baterako joera sumatzen zaio; nonbait, aldagai baten balio altuei bestearen balio altuak dagozkie, eta baxuei baxuak, eta, gainera, proportzionalki adierazten dira. Erlazio lineal hori ez da erabat zehatza (puntuak ez daude erabat lerrotuta). Estatistiko bat definitzen da erlazio horren indarra neurtzeko, korrelazio linealaren koefiziente deritzona, edo korrelazio-koefiziente besterik gabe (sinplifikazio horrek badu arrisku bat, zenbaiti "linealaren" ahaztu egiten baitzaio, eta, ondorioz, interpretazio okerrak eragiten).
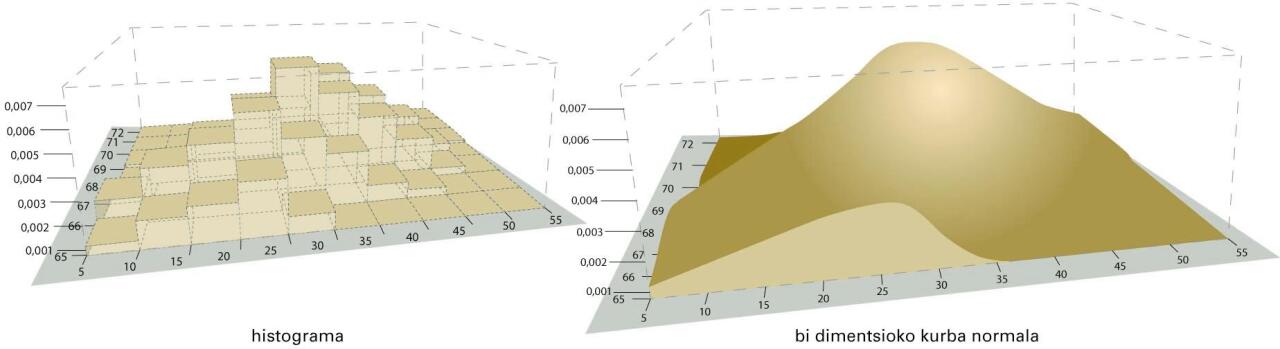
Joera lineal horrez gain, maiztasun handienak erdialdean agertzen dira, eta pixkanaka txikiagotuz joaten dira erdialde horretatik urrundu ahala. Aurreko diagraman, maiztasunen neurria biribilen tamainaz adierazi da. Ondorengoan, aldiz, altueraren bidez: maiztasun-taulari dagokion histograma ageri da.
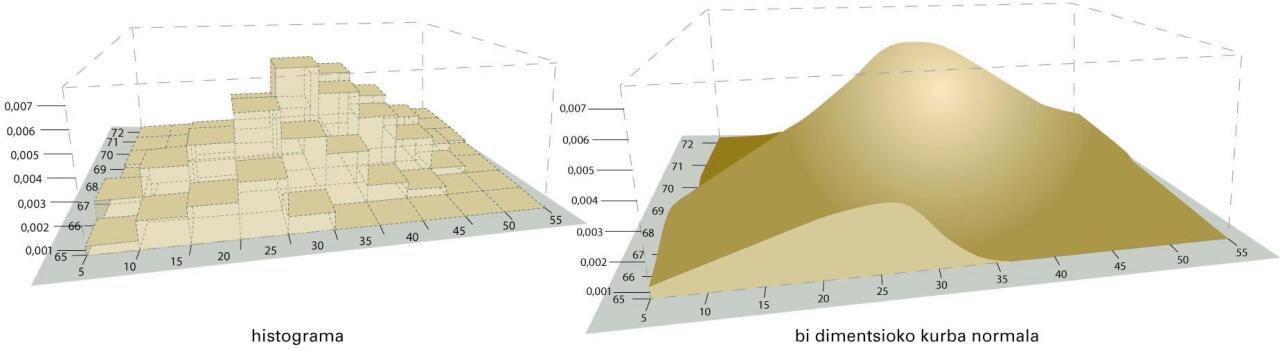
Halako egoera batean, bi dimentsioko eredu normala egokitzea bidezkoa da. Eredu horrek bi aldagaien arteko informazio guztia mamitzen du bost parametroren balioetan. Gainera, propietate matematikoen ikuspegitik, esan beharra dago lotura estua dagoela bi aldagaien bost estatistiko edo adierazleren (bi batezbestekoak, bi desbideratze estandarrak eta korrelazio-koefizientea) eta bi dimentsioko eredu normalaren bost parametroren artean. Kasu honetan, eta bakarrik kasu honetan, korrelazio linealaren koefizienteak zero izateak adierazi nahi du aldagaien artean ez dagoela erlaziorik, independenteak direla alegia.
Eredu normala: histograma eta bi dimentsioko kurba normala
Eredu normalak zerikusi handia izan du estatistikaren garapenean, baina, orobat, esan behar da ez dela beti bidezkoa izaten eredu horren egokitzapena (gutxitan baizik), eta, beraz, tentu handiz erabili behar direla halako tresnak: itxuroso eta erosoak dira, baina informazioa desitxura dezakete behar ez denean erabiliz gero. Gaur egun, konputazioaren bilakaerak teknika berriak ekarri ditu datuen azterketara.
Aldagai anitzen arteko erlazioaren analisia
Errealitateko problema gehienetan, aldagai anitz (p) hartzen dira kontuan. Haien arteko erlazioak aztertzea ez da lan samurra, ezin baitira aztertu binaka hartuta ateratzen diren guztiak (p(p-1)/2 binakako azterketa-kopurua), eta are gutxiago hirunaka edo gehiagonaka hartuta ateratzen diren erlazio guztiak. Ezinbestekoa da teknika miatzaileak garatzea, konbinatoria zabal hori murriztearren. Datu-analisiaren arrakasta teknika horien garapenean datza.
Aldagai anitzen arteko erlazioak aztertzeko garatutako tresnen oinarri nagusiak bi aldagairen artekoen kasukoak berak dira. Aniztasunaren aurrean datu-analisian erabiltzen diren teknikak bi motatan sailka daitezke: aldagai guztien arteko erlazioak bilatzen dituztenak, eta aldagai bat edo batzuen aldagarritasunaren zergatia azalarazteko erlazioak bilatzen dituztenak. Lehen motakoak dira, esate baterako, faktore-analisia, dimentsio anitzeko mailaketa, mordokako analisia edo sailkapen automatikoa (cluster analysis); bigarrenekoak, berriz, bariantza-analisia, erregresio-analisia, analisi bereizlea (discriminant analysis), erabakitze-zuhaitzak, k-auzokide gertuenak eta abar. Badira teknika batzuk, propio egokituz gero, bi zereginetarako erabiltzen direnak: sare bayestarrak eta neurona-sareak, esate baterako.
Ia teknika guztiak aldagai-mota bakar baterako sortu dira, kuantitatiboetarako edo kualitatiboetarako. Aldagai kuantitatiboak kualitatibo bihur daitezke kategorizatuz, eta galdutako informazioa (erlazioak) azterketaren azken urratserako gordez; baina alderantzizkoa ezinezkoa da, ez bada aldagai kualitatiboen arteko erlazioak zenbaki bihurtzeko bidetik egiten. Aldagai kuantitatibo bat kategorizatzeko modua, bestalde, ez da bakarra, eta, beraz, problema berri bat planteatzen da. Horrekin guztiarekin esan nahi da, aldagai anitz aztertzeko, teknika bat erabili aurretik beste azterketa batzuk egin beharra dagoela.
Gero, teknika horiek erabiltzean lortzen diren emaitzek beste bi gai jartzen dituzte mahai gainean: haien ulergarritasuna eta baliozkotasuna. Bi arazoen garrantzia problema errealaren araberakoa da. Dena dela, bi gai horietarako ere badira berezko teknikak datu-analisiaren alorrean.
Aipatutako teknika horiek guztiak erabili ahal izateko, ezinbestekoa da konputagailua.
DATU-ANALISIA ETA KONPUTAZIOA
Halako kalkuluak eta diagramak egiteko, konputagailua ezinbestekoa gertatzen da. Zer esanik ez aldagai asko batera aztertzen direnean.
Konputagailuen garapenak (softwarearenak eta hardwarerenak) datu-analisiari ekarri eta ekartzen diona funtsezkoa da. Hain da funtsezkoa, ezen gaur egun ia ezin baita bereizi datu-analisiaren gaia bera estatistikakoa den (hitz hori esanahi tradizionalean ulertuta) edo konputaziokoa. Konputagailuen bitartez, informazioa landu egiten da (informatika izena horri zor zaio, izan ere), eta lantze horren alor bat informazioa bilatzea da, hain zuzen, datu-analisiaren zeregina. Datu-analisia horregatik dago hain lotuta konputagailuaren alorrak hain bereak dituen datu-base, adimen artifizialeko ikasketa automatiko (machine learning), formen ezagutza (pattern recognition), bistaratze zientifiko eta abarrekin. Datu-analisiaren metodologia, ordea, estatistikarena da.
Aldagai anitzeko azterketan aipatutako teknika gehienak konputagailua izanda egin dira, ezin baita halakorik erabili konputagailurik gabe. Aspaldi, konputagailuak sortu aurretik, datuen analisian egin beharreko konputazio edo kalkuluak egiteko, datuei atxikitako hipotesi mordo baten ondorioz lortutako formula analitikoak erabiltzen ziren, eta horiek, gainera, muga batzuk zituzten. Azken urteotan, datuen azterketa halako hipotesirik gabe egin daiteke, konputagailua eta berezko algoritmoak erabiliz. Alderdi horretatik, gaur egungo analisi-mota lehenagokoa baino egokiagoa da, konputagailuen garapenari esker.
Informazioa bistaratzeari dagokionez ere, izugarrizko aurrerapena izan dugu konputagailuei esker. Ohiko grafikoak modu programatu eta errazagoan egiteaz gain, kalitate handiagokoak izan daitezke: besteak beste, koloreak, formak, dinamismoa eta elkarrekintza ahalbideratzen baitituzte konputagailuek.
Konputagailuen etorkizuneko ahalmen berriek datuak aztertzeko teknika berriak lortzera ere bultzatuko dute. Datu-analisiaren etorkizuna, beraz, konputagailuen bilakaeraren menpe dago, orain dela gutxi arte analisi matematikoaren eta aljebraren menpe zegoen bezala.