estatistika
- 1. Estat.
Unitate-multzo edo pertsona-multzo bati dagozkion zenbakizko datuak biltzen, sailkatzen eta aztertzen dituen zientzia; delako zenbakizko emaitzak berak. Erabat ezagunak ez diren gertaera kolektiboen zenbakizko azterketa egiteko analisi matematikoa (eragiketak, teknikak, eta metodoak) da estatistika.
- en statistics
- es estadística
- fr statistique
1. Estat.
-

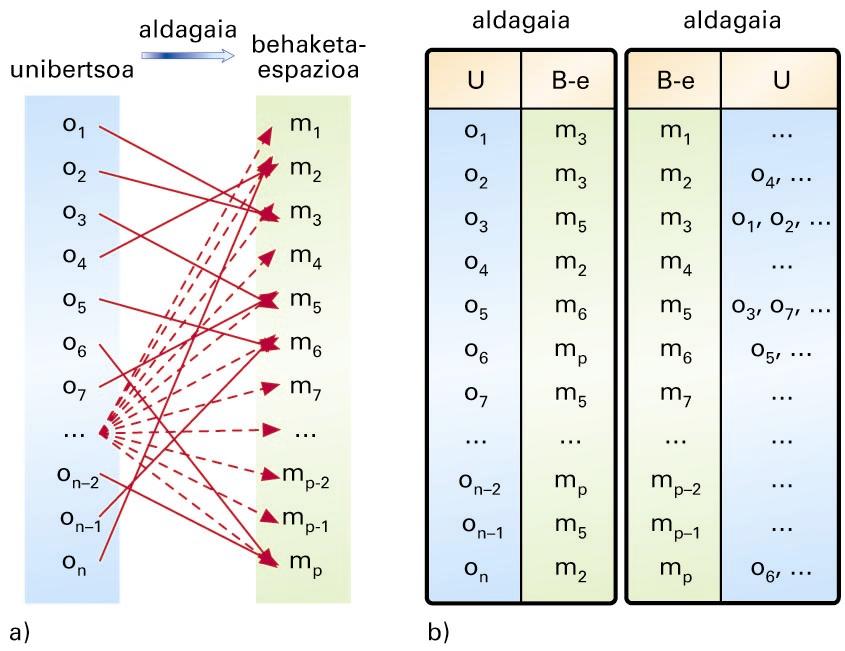
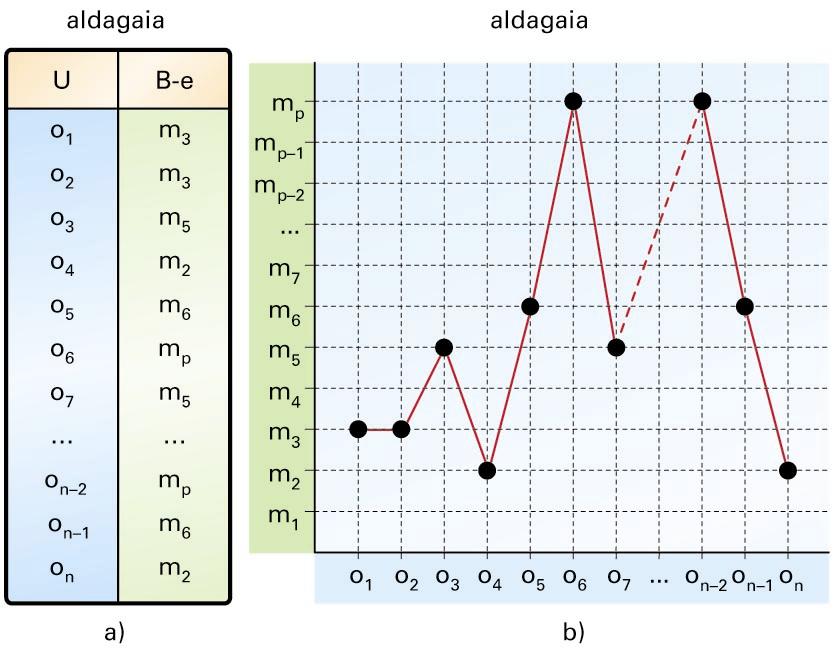
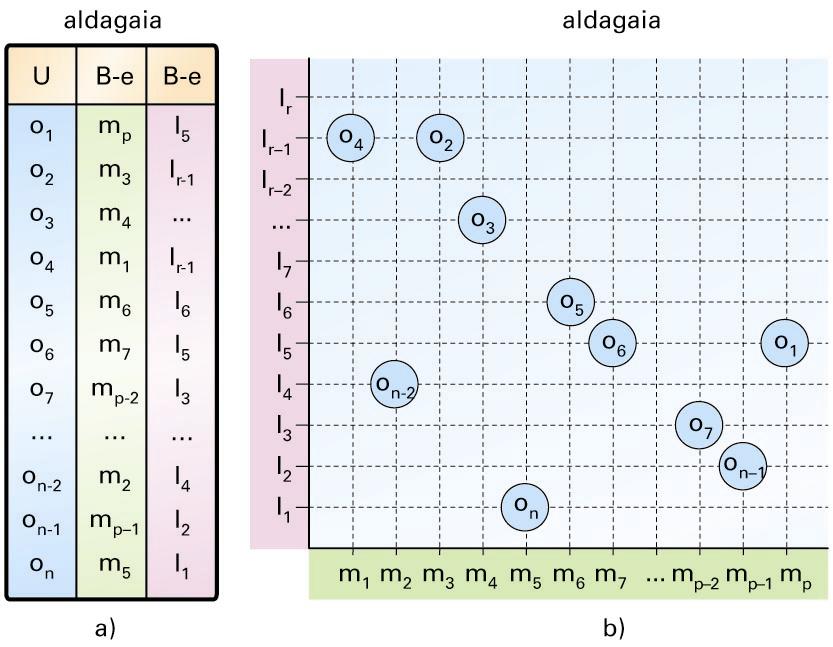
a) Behaketa-prozesua; b) datu gordinen taula -
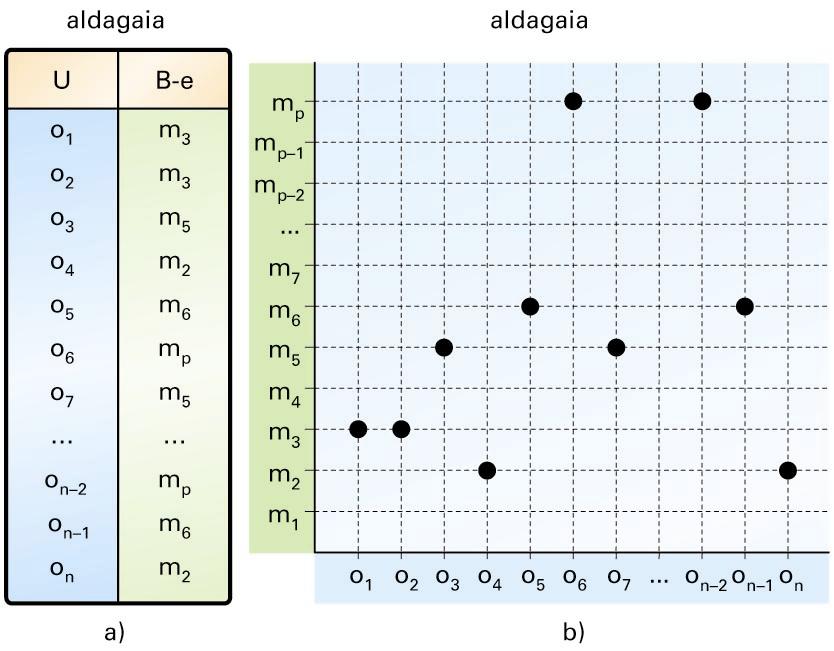
a) Datu gordinen taula; b) datu gordinen taulari dagokion oinarrizko diagrama -
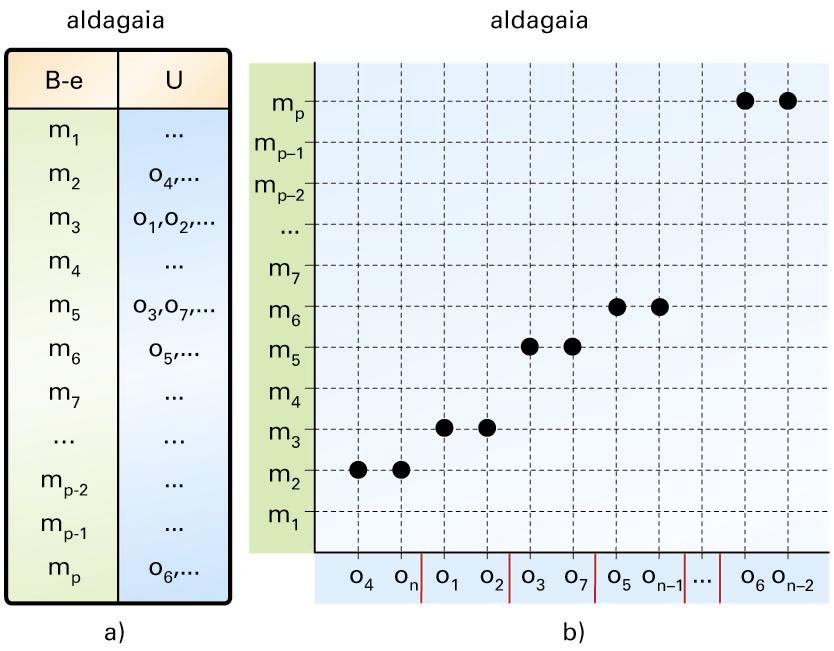
a) Datu gordinen taula; b) aldagai batek unibertsoari eragiten dion partiketa -
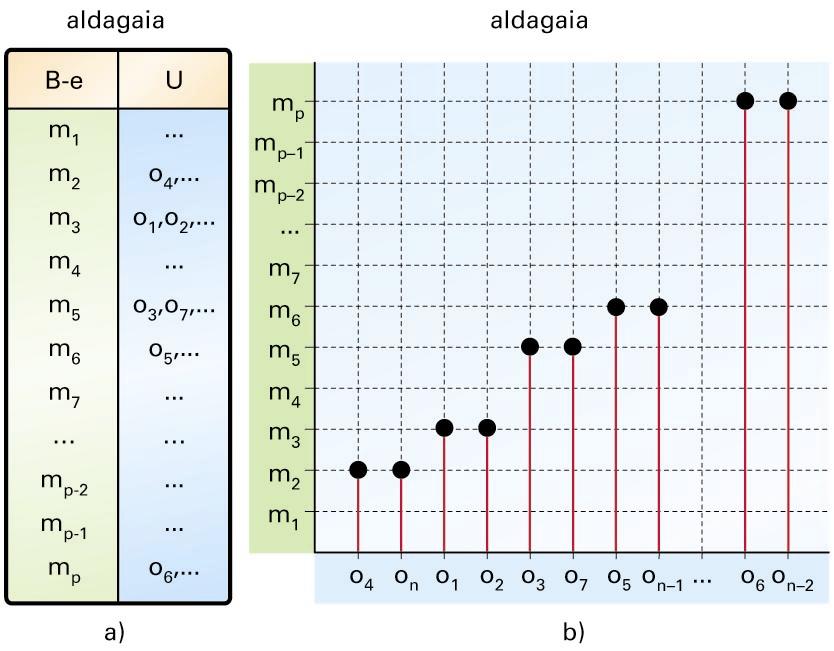
a) Datu gordinen taula; b) zenbakizko aldagai batek unibertsoari eragiten dion egitura -
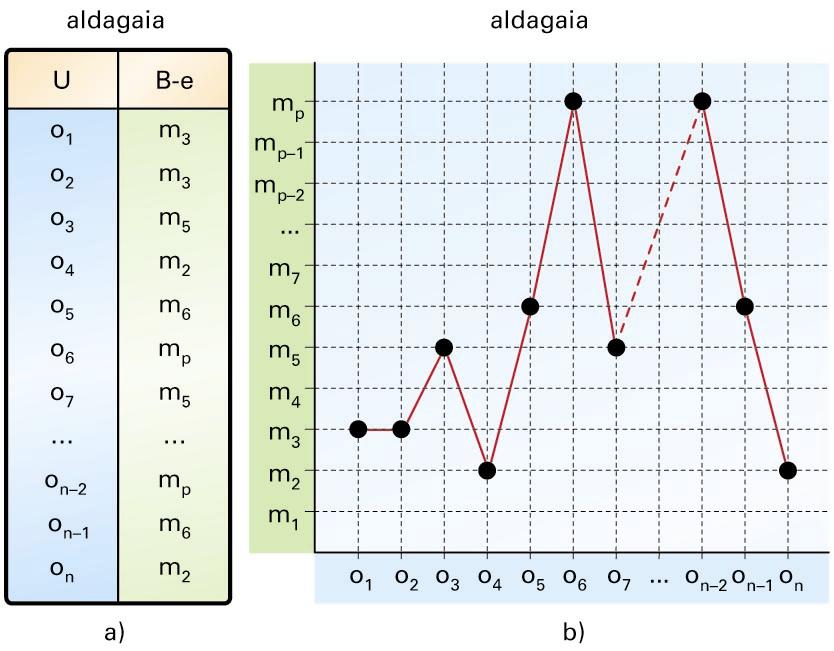
a) Datu gordinen taula; b) marra-diagrama: unibertsoaren eta behaketa-espazioaren ordenazko egituren arteko aldagaia -
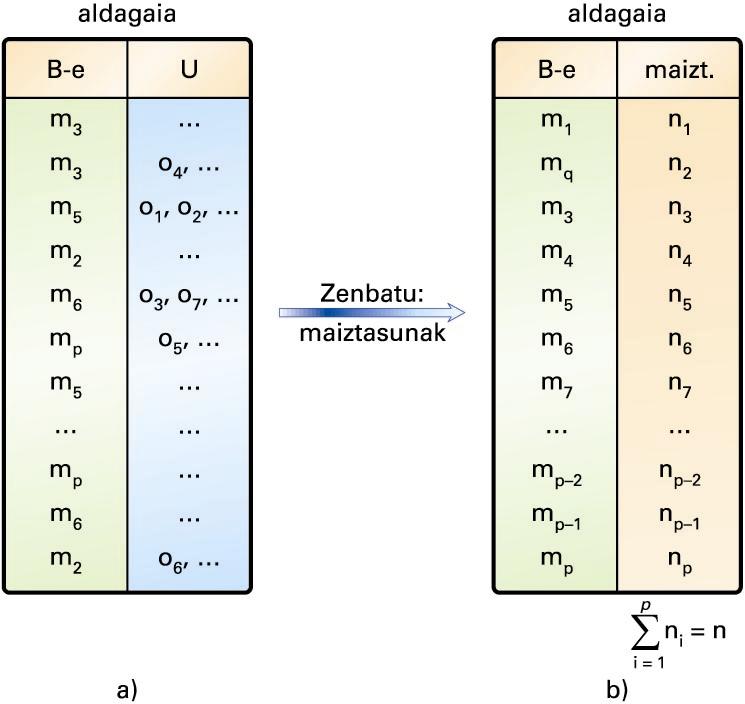
a) Datu gordinen taula; b) maiztasunen taula -
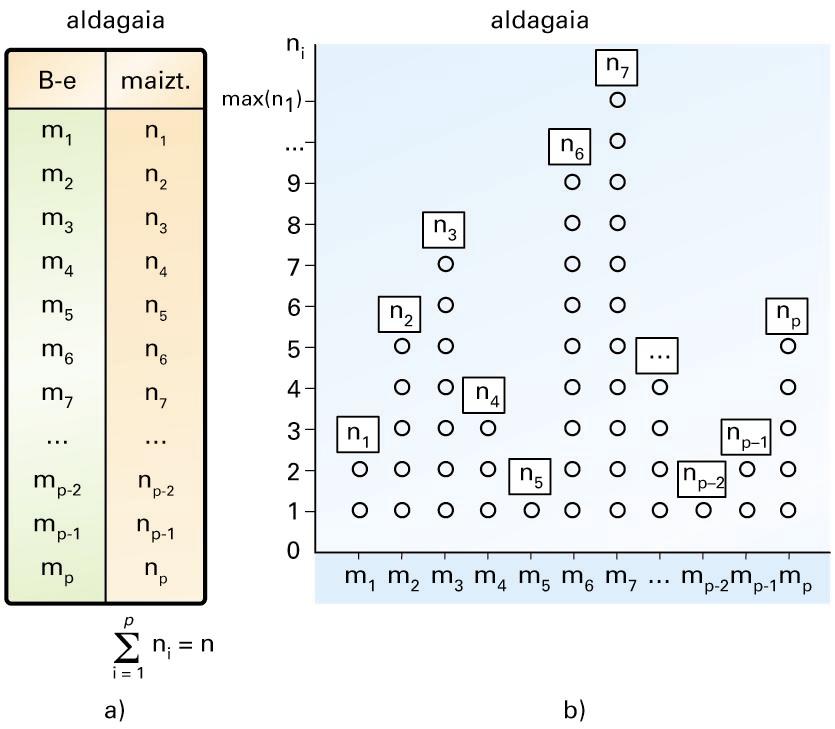
a) Maiztasunen taula; b) maiztasun-taularen diagrama -
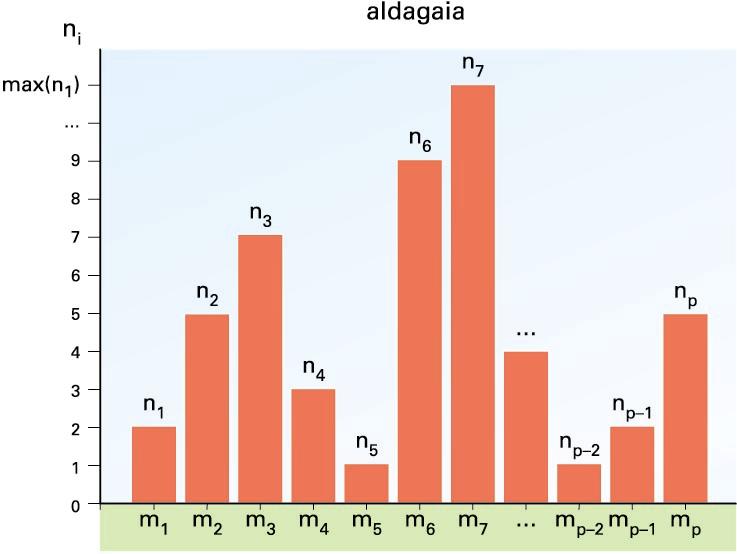
Barra-diagrama. Behaketa-espazioaren egitura: ordenazkoa -
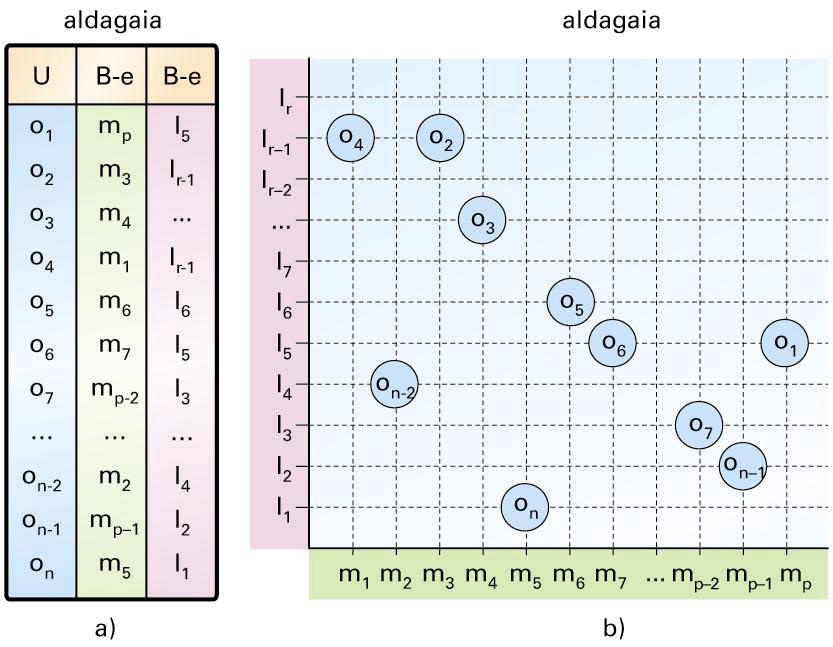
a) Datu gordinen taula; b) datu gordinen taulari dagokion oinarrizko diagrama -
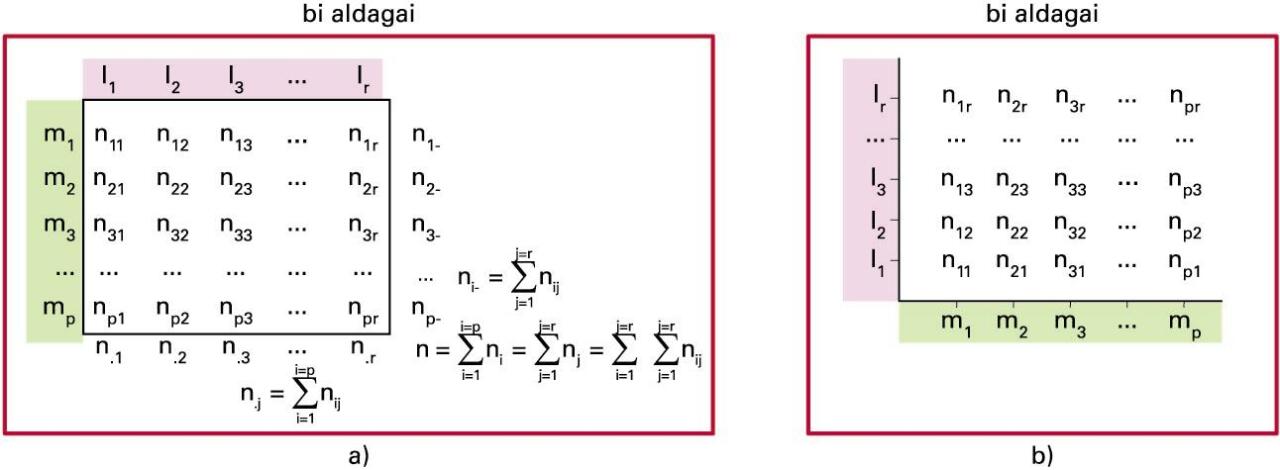
a) Maiztasunen taula; b) maiztasunen taulari dagokion oinarrizko diagrama -
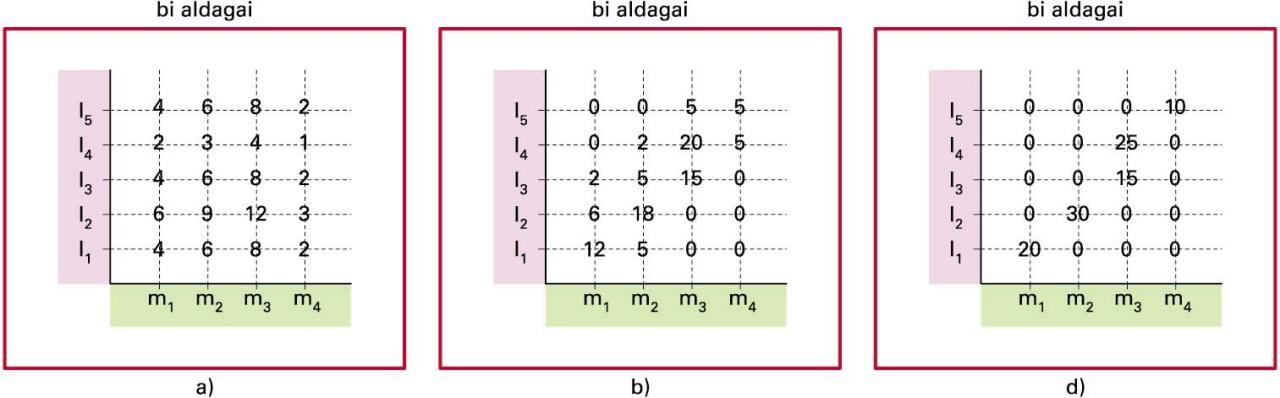
a) Independentzia: nnij = nj.nj.j; b) nolabaiteko menpekotasuna; d) erabateko menpekotasuna: nij = nj edo f(lj) = mi
- 1. Estat.
- Unitate-multzo edo pertsona-multzo bati dagozkion zenbakizko datuak biltzen, sailkatzen eta aztertzen dituen zientzia; delako zenbakizko emaitzak berak. Erabat ezagunak ez diren gertaera kolektiboen zenbakizko azterketa egiteko analisi matematikoa (eragiketak, teknikak, eta metodoak) da estatistika.
Estatistika Edit
Egilea: Yosu Yurramendi
Errealitatearen inguruko arazo bati buruzko erabakiak hartzen laguntzeko, sarritan, informazioa biltzeari ekiten zaio. Informazioa biltzeko modu bat arazoaren menpean dauden objektu guztiak (edo batzuk) behatu eta datuak biltzea izaten da.
Datu-multzo bat bildu, aztertu eta bere baitan daraman informazioa azaldu eta aurkezteko erabiltzen diren metodo, tresna eta ikerketa matematikoak dira estatistika izena duen jakintza-arloa osatzen dutenak.
Estatistika errealitateko jakintza-alor batean erabiltzen denean, estatistikak egiten dira. Beraz, estatistikak egitearen helburua da errealitatearen inguruko arazo bati buruzko erabakiak hartzen laguntzea.
Estatistika eta estatistikak
Estatistikak jakintza-arlo gehienetan egiten dira, ekonomian eta medikuntzan, meteorologian eta psikologian, hizkuntzalaritzan eta administrazioan, informatikan eta genetikan, nekazaritzan eta kirol-arloan. Behaketa eta saiakuntzetatik lortzen diren datuetan oinarritzen diren jakintza-motek estatistikan aurkitzen dute informazioa lantzeko eta ondorioei kutsu matematiko edo objektiboa emateko metodologia eta tresneria.
Eta alderantziz, jakintza-arloen berezitasunek bultzatzen dute estatistika-tresna eta -metodo berriak ikertu eta burutzea. Abstrakzio horren ondorioz, beste jakintza-arloetan antzeko datu- eta problema-motak azaltzen direnean, lehenago baliatutako tresna eta metodoak erabiltzen dira informazioa lantzeko. Zentzu horretan, estatistika beste jakintza-arloekin duen elkarrenganako menpekotasunean datza, matematiketako beste arlo asko bezala.
Estatistikan aritzen denari estatistikari esaten zaio. Estatistikak egiten dituztenak arlo jakin bateko adituak izaten dira, dela maila batean edo bestean estatistika ongi dakitelako, dela estatistikari baten laguntza dutelako. Problema baten aurrean, estatistikarien zereginak hauek dira: estatistikako teoria eta metodologiak aztertu, egokitu eta hobetu; datuak biltzeko moduaz aholkuak eman; datuak balioztatu, landu, aztertu eta interpretatu; azterketaren ondorengo emaitzak txosten estatistikoan argitaratzeko aholkuak eman.
Estatistikaren ezagutzaren bat izatea ia ezinbestekoa bihurtu da gaurko informazioaren gizartean. Non-nahi azaltzen dira estatistikak, eta, sarritan, tamalez, nolanahi. Estatistikak azaltzen dira edozein gairen inguruan, nonbait objektibotasun-kutsua emateko, eta jakinda zenbakien inguruan izugarrizko ezjakintasuna dagoela. Inpresio aski zabaldua da, bestalde, egilearen mesedetan egin eta erabiltzen direla estatistikak, besteak beste, gai berari buruzko estatistika kontrajarriak azaltzen direlako egilearen arabera; ondorioz, mesfidantza handia sortzen dute.
Horren aurrean, estatistikaren ezagutza zabaltzea eta sakontzea da irtenbidea. Ezagutza hori hiru mailatan sailka daiteke:
Maila arrunta, gaur egun biztanle orok eduki beharko lukeena komunikabideetan adierazten direnak jaso ahal izateko eta bizimodu arrunteko zenbait gai kudeatzeko (tartean, etxeko ekonomia); ondorioz, hezkuntza-sisteman berezko tokia izan beharko luke ikasgai gisa.
Jakintza-arlo jakin baterako ezagutza-maila, hezkuntza-sistemaren goiko mailetan ikasten dena.
Maila berezia edo goi-maila, estatistikariei dagokiena eta unibertsitateetako estatistika-sailen inguruan gauzatzen dena, matematikako titulazioaren adar gisa edo estatistikako berezko titulazio moduan.
Nahiz jakintza-arlo gehienen bilakaera laguntzeko estatistikak egiten diren, estatuen antolakuntzan jarduten diren erakunde ofizialenak dira ezagunenak, estatistika ofizialak, alegia. Hona hemen erakunde horietako batzuk: EUSTAT (Euskal Estatistika Erakundea), Instituto de Estadística de Navarra, INSEE (Institut National de la Statistique et des Études Économiques), INE (Instituto Nacional de Estadística), EUROSTAT (Statistical Office of the European Communities), United Nations Statistics Division, UNESCO Institute for Statistics eta, oro har, 1885an sortutako ISI (International Statistical Institute) erakundearen direktorioan zerrendatzen direnak.
Oinarrizko kontzeptuak
Estatistika eta estatistiken muina bi kontzeptu nagusi hauek osatzen dute: unibertsoa eta behaketa-espazioa.
Unibertsoa (estatistikako tradizioan populazio esaten zaio; aurrerago azalduko da horren zergati historikoa) arazo edo problemaren menpean dauden objektuek osatzen dute; behaketa-espazioa, aldiz, problema ebaztearren objektuei behatzen zaizkien ezaugarriek.
Objektuei ezaugarri bat behatzean antzeman daitezkeen era edo modalitate ezberdinek osatzen dute behaketa-espazio bakoitza. Modalitateek estatistikak egiteko beharrezkoa den aldagarritasunaren oinarria adierazten dute.
Unibertsoko objektuen artean egon daitezkeen erlazioak, hau da, unibertsoaren egitura (edo egiturarik eza) estatistikaren aztergai bat da, baita behaketa-espazioen egiturak ere, modalitateen artean egon daitezkeen erlazioak, alegia. Estatistikak egiteko kontuan hartu eta, beraz, aldez aurretik zehaztu behar diren gaiak dira errealitatearen inguruko arazo jakin baten unibertsoaren egitura, eta horko objektuei behatu behar zaizkien espazioen egitura zehatzak. Erlazio horiek guztiak aldez aurretiko datuak dira; hau da, aldez aurretiko informazioa.
Estatistika, aldez aurretiko datuetan oinarrituta, erlazio berriak bilatu eta aurkezteko bidea da, eta berezko jakintza-arlo gisa hartzen da, jakintza-arlo ezberdinetako arazoen unibertsoaren eta behaketa-espazioen egiturak berberak direnean bide berberak eskaintzen dituelako. Abstrakziora eta formalizaziora jotzeko ahalegin horren zentzuan, matematika aplikatuko adartzat har daiteke estatistika. Bestalde, egia da estatistikaren objektu matematikoak ez direla berezkoak, geometriakoak, aljebrakoak edo analisikoak baizik, eta horietatik maileguz hartzen dituela; ondorioz, batzuen ustez, ez dago funtsik matematikaren adartzat hartzeko.
Estatistikak, datuak bildu eta estatistikaren bidea ibiliz, aurretiko eta aurkitutako erlazio berriak dira. Horiexek osatzen dute estatistikaren bitartez bilatzen den informazioa.
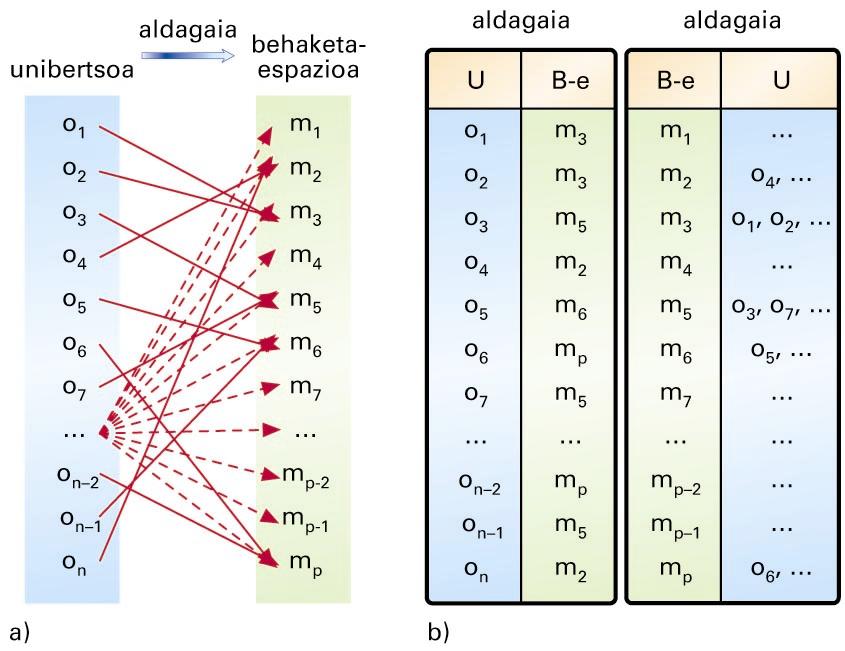
Datuak biltzea da unibertsoko objektu bakoitzari behaketa-espazio bakoitzeko modalitate bat egokitzea. Unibertsoaren eta behaketa-espazioaren arteko egokitzeari aldagai deritzo. Aldagai baten ondorioz, datu gordinen taula antolatzen da, objektu bakoitzaren aldamenean dagokion modalitatea azaltzen duena. Alderantzizko taula ere antola daiteke, modalitate bakoitzari egokitutako objektuak azalduz.
a) Behaketa-prozesua; b) datu gordinen taula
Datuak aztertzea da, alde batetik, erlazio berriak ezartzea: bai unibertsoko objektuen artean, bai behaketa-espazioko modalitateen artean, baita objektuen eta modalitateen artean ere; eta bestetik, erlazio nabarmenenak agerian utziz eta axalekoak baztertuz, datuek beren baitan daramaten informazioa mamitzea. Datuak aztertzearen helburua da, labur esanda, datu guztien irakurketa bakar baten ondoren ulertzeko zaila den erlazio-zerrenda luze batetik informazio egokia erauzi edo ateratzea.
Diagrama edo grafikoak oso lagungarri gertatzen dira erlazioak ulertzeko garaian.
a) Datu gordinen taula; b) datu gordinen taulari dagokion oinarrizko diagrama
Datuen azterbidea aldagaiaren bitartez egiten da. Aldagaiaren bidez, unibertsoaren egitura (halakorik balego) behaketa-espazio(eta)ra igarotzen da, eta alderantziz, behaketa-espazio(eta)ko egitura(k) unibertsora.
Unibertsoa eta behaketa-espazioa, biak, egiturarik gabekoak badira ere, behaketa-espazioak partiketa edo sailkaketaren egitura eragiten dio unibertsoari, baliokidetasun-erlazio bat, alegia; erlazio horren arabera, modalitate bera duten objektuak parte edo sail berekoak dira, hots, baliokideak.
a) Datu gordinen taula; b) aldagai batek unibertsoari eragiten dion partiketa
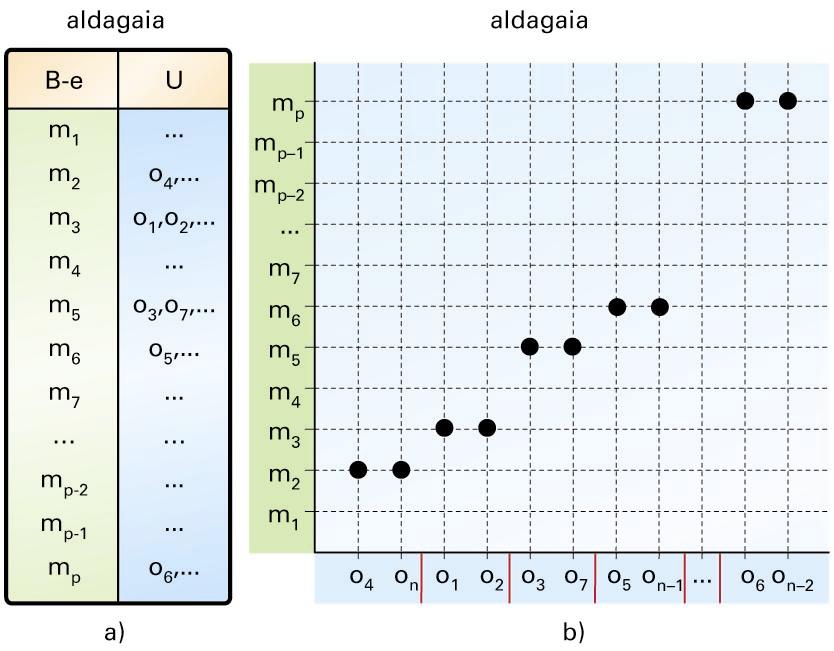
Behaketa-espazioa egituratuta baldin badago, esaterako, modalitateen artean ordena bat definituta badago, orduan, ordena hori unibertsora igarotzen da aldagaiaren bitartez, eta, aldagai horren arabera, bi objektu, edozein, alderatu daitezke ezartzeko bietatik zein objektu dagoen bestearen aurretik (edo parean). Ordenaz gain, neurri-unitate bat ere egon daiteke definitua behaketa-espazioan (zenbakizkoa izango da, beraz). Orduan, unibertsoan neurriaren egitura hori islatzen da.
a) Datu gordinen taula; b) zenbakizko aldagai batek unibertsoari eragiten dion egitura
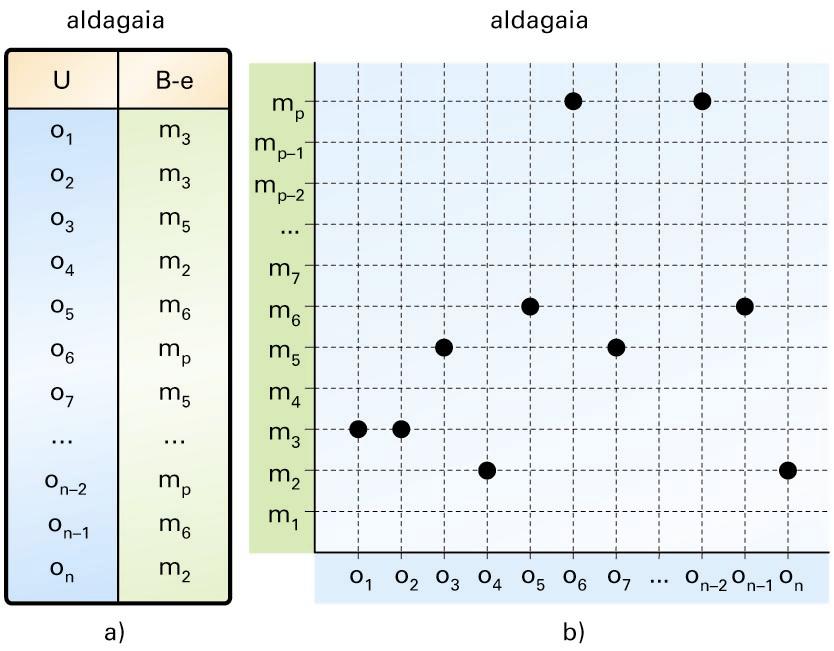
Unibertsoa egituratuta baldin badago, estatistikaria saiatzen da egitura horren berezitasunari berezko bideak egiten, behaketa-espazioko modalitateak egitura horretan nola sakabanatzen diren antzematearren. Bide horiek ibiliz uzta biltzea estatistikak egitea da. Adibidez, unibertsoaren egitura ordenazkoa izan daiteke:
a) Datu gordinen taula; b) marra-diagrama: unibertsoaren eta behaketa-espazioaren ordenazko egituren arteko aldagaia
Are gehiago, ordenaz gain, neurri-unitate bat egon daiteke definituta, eta, orduan, egitura lineala da (denbora, kasu). Unibertsoaren egitura plano batean ere, bi dimentsiotan, egon daiteke definituta; esate baterako, mapa geografikoak eta argazkiak.
Unibertsoaren tamaina txikia denean (hori erlatiboa da oso; hala dela jo daiteke, objektuen identitatea kontuan hartzekoa denean bilatzen den informaziorako), behaketa-espazio horren (horien) ondorioz objektuek elkarren artean azaltzen d(it)u(z)ten erlazio berria(k) d(ir)a interesgarria(k). Baina unibertsoaren tamaina handia denean (objektuen identitatea garrantzi handikoa ez denean), behaketa-espazio(et)an jartzen da arreta estatistikoa.
Unibertso handi horretan ez badago egiturarik, aldagaiaren bitartez modalitate bakoitzari objektu-kopuru bat egokitzen zaio, unibertso horretan modalitate hori zenbat objekturi egokitu zaien, hau da, zenbatetan gertatu den adierazten duena. Frekuentzia edo maiztasun deritzo horri.
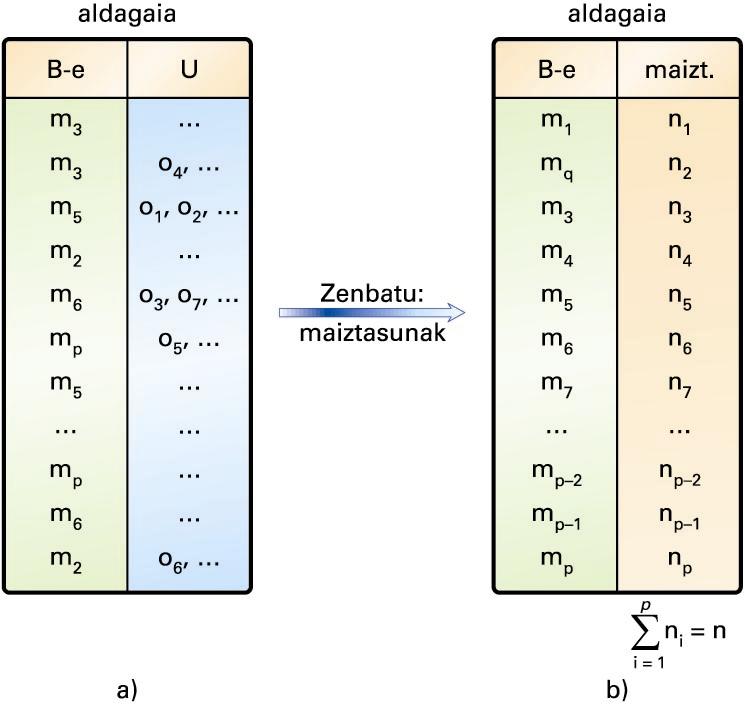
a) Datu gordinen taula; b) maiztasunen taula
Maiztasunaren arabera, behaketa-espazio bateko modalitateei erlazio berri bat ezartzen zaie, neurri batek definitzen duena, alegia. Aipatutako alderantzizko ikuspegiari esker ere, erlazio berri bat ezartzen zaie unibertsoko objektuei ere.
Maiztasunak kalkulatzen direnean, estatistikaren aztergaia, batez ere, aldagarritasunaren nondik norakoa da, hau da, behaketa-espazioen modalitateen maiztasunen banaketak; aldagaien banaketak, labur esanda. Horixe da historian zehar estatistikan gehien jorratu den gaia.
Kontuan hartzekoa da modalitateei maiztasun bat (zenbaki ez-negatibo bat) egokitzen zaienean problemaren ebazpenean, nolabait esateko, koska edo maila bat gora egiten dela: behaketa-espazioa unibertsotzat hartzen da, eta modalitateei maiztasuna behatzen zaie.
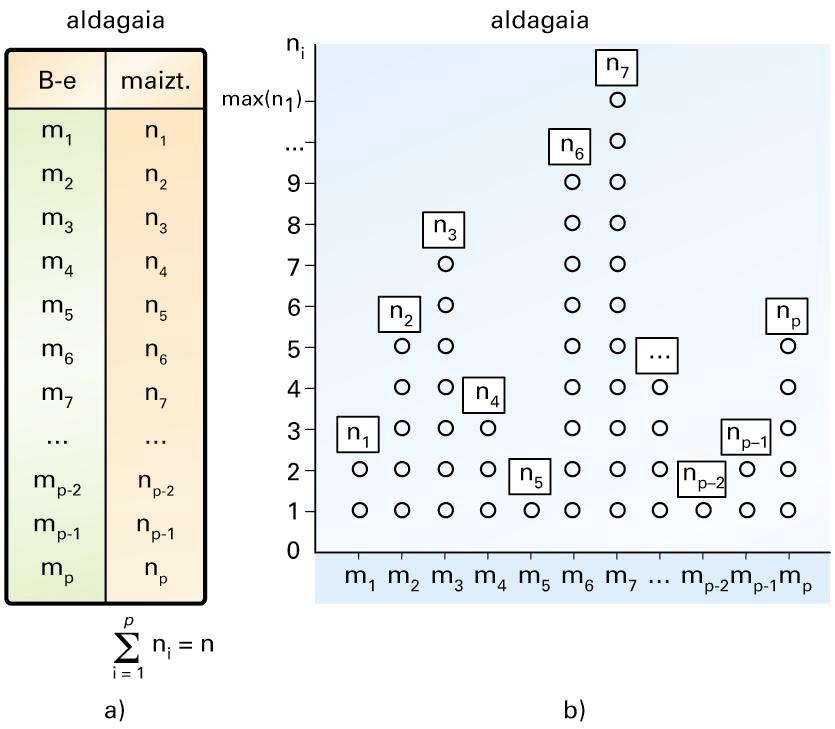
a) Maiztasunen taula; b) maiztasun-taularen diagrama
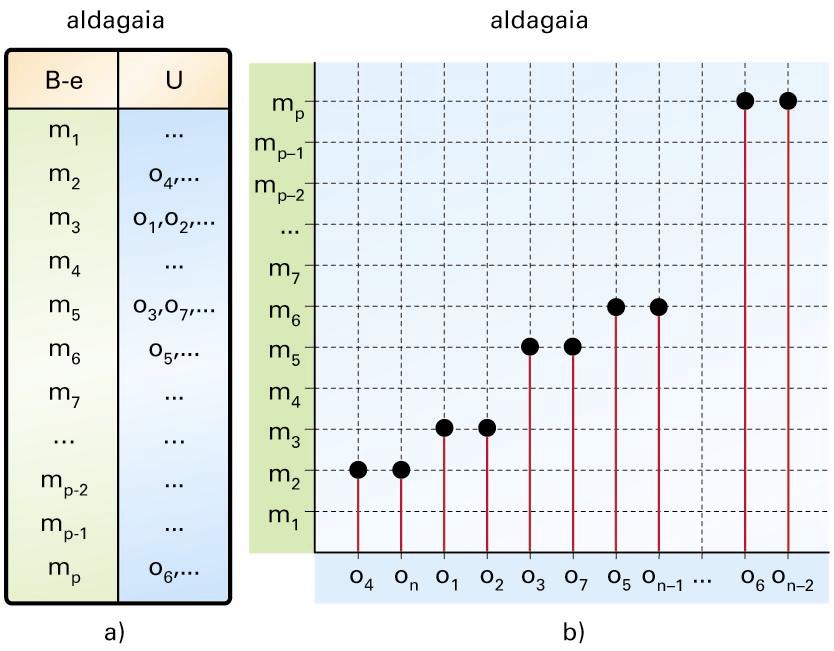
Unibertsoa handia denez, maiztasuna dagokion diagraman objektu bakoitzeko puntu batez adierazi baino, lehen azaldutako marra-diagrama batez adierazten da: modalitateei (aipatutako goi-mailako unibertso berriko objektuei) maiztasunaren neurriari dagokion luzerako marra bana egokitzen zaie. Ohituraz edo, goi-mailako kasuetan, maiztasunak barren (marra zabalen) bitartez adierazten dira.
Behaketa-espazioak egiturarik ez badu, ohikoa da diagraman maiztasunaren arabera ordenatzea modalitateak (handienetik txikienera, edo alderantziz), baina, ordenarik baldin badu, egitura horri eutsi behar zaio. Modalitateen artean neurri-unitate bat definituta egongo balitz, horri ere eutsi beharko lioke diagramak.
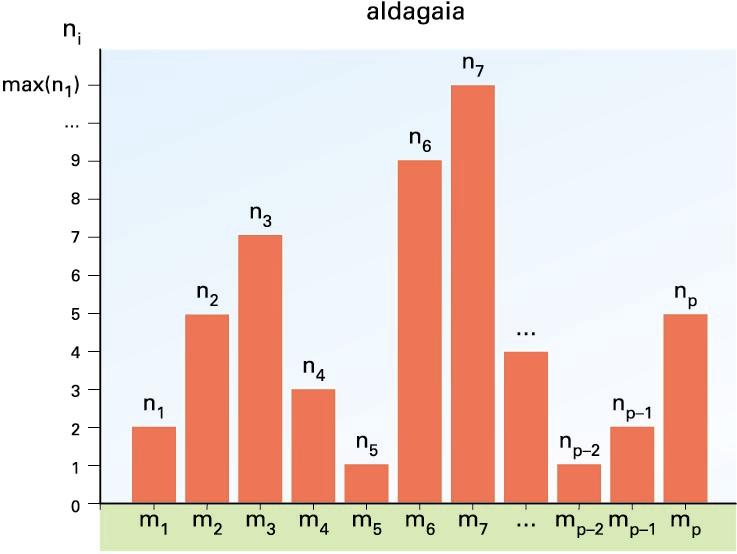
Barra-diagrama. Behaketa-espazioaren egitura: ordenazkoa
Gehienetan, aldagaien banaketak, maiztasun hutsen bitartez adierazi beharrean, hobeto ulertze aldera, maiztasun erlatiboez adierazten dira: ni baldin bada mi modalitateari dagokion maiztasun absolutua, ni / n da unibertso osoarekiko bere maiztasun erlatiboa (0 eta 1 zenbakien arteko zenbaki bat), edo ehunekotan (%), hizkera estatistiko arruntagoa erabiliz, 100 · ni / n. Maiztasun hutsei maiztasun absolutu esaten zaie, nonbait maiztasunaren bi izenlagunak parez pare jartzearren.
Ondorioz, gehienetan maiztasun erlatiboak erabiltzen dira aldagaiaren banaketari dagozkion maiztasun-taula eta barra-diagrama eraikitzeko. Dena dela, maiztasun absolutuek izan izaten dute berezko garrantzia zenbait kasu praktikotan.
Azterketan bi aldagai hartzen direnean kontuan, hau da, objektuak bi espazioren arabera behatzen direnean, erlazio konplexuagoak bilatzen dira.
Unibertsoaren tamaina txikia denean, bi behaketa-espazio horien ondorioz objektuek elkarren artean azaltzen duten erlazio berria da interesgarria.
a) Datu gordinen taula; b) datu gordinen taulari dagokion oinarrizko diagrama
Unibertsoaren tamaina handia denean, aldiz, bi behaketa-espazioen arteko erlazioa da arreta estatistikoa eragiten duena.
Unibertso handi horretan ez baldin badago egiturarik, berriz, bi behaketa-espazioen modalitate-bikote bakoitzari egokitzen zaion maiztasuna da azterbidearen euskarria.
Bi behaketa-espazioren arteko erlazioaren azterketa bi espazio horietako modalitate-bikote bakoitzari egokitzen zaion maiztasunean datza. Horien bitartez, bi espazioen arteko erabateko menpekotasuna zer den definitzen da, baita beste muturrean dagoen erlaziorik eza (independentzia) ere. Bi muturren artean, kasuistika zabala erakuts dezakete maiztasunek, eta estatistikaren zeregina da gertatutakoa zein bi muturren ondoan (eta zein ondoan) gertatu den bilatzea eta adieraztea.
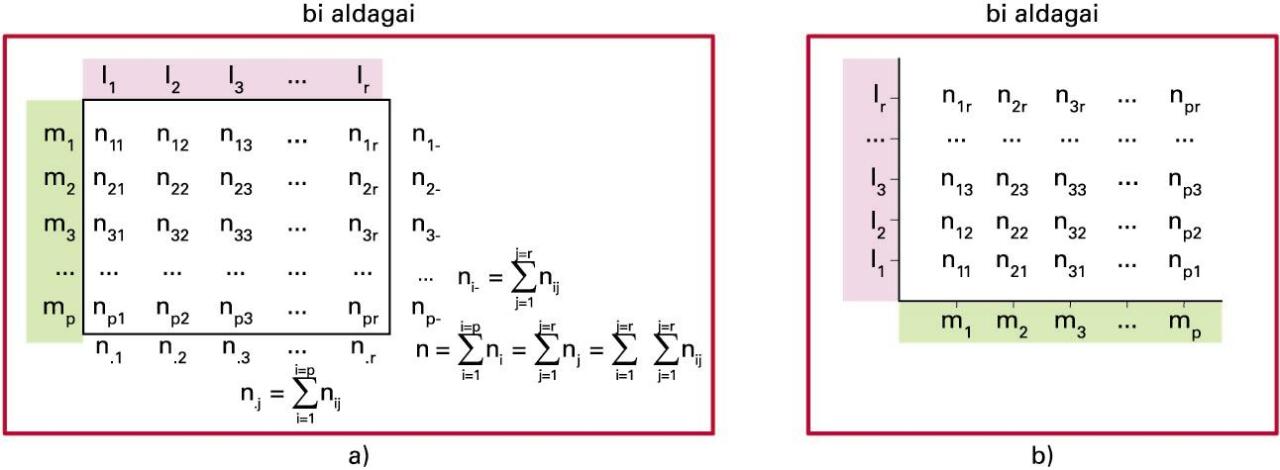
a) Maiztasunen taula; b) maiztasunen taulari dagokion oinarrizko diagrama
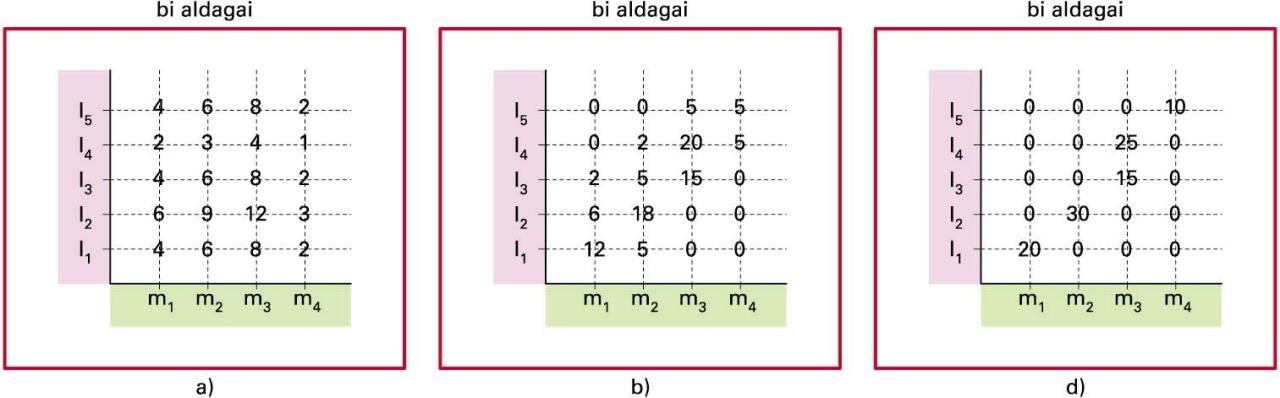
a) Independentzia: nnij = nj. nj.j ; b) nolabaiteko menpekotasuna; d) erabateko menpekotasuna: nij = nj edo f(lj) = mi
Gehienetan, aztergaia den errealitateko arazoaren inguruan bi behaketa-espazio baino gehiago izaten dira. Guztien modalitateen arteko erlazioak bilatzeko, modalitate-hirukoteak, -laukoteak eta abar aztertu beharko lirateke, baina ezinezkoa da, alde batetik, konbinatorioki zabalegiak izan daitezkeelako, eta bestetik, maiztasunak txikiegiak direlako. Orduan, estatistikaren azterbidea izaten da arazoaren espazio-aniztasun hori murriztea, ahalik eta informazio gutxien galduz (horretarako, noski, informazio-neurriren bat definitu beharra dago), eta espazio murritz horretan erlazio garrantzitsuenak bilatzea. Hori guztia egiteko, oinarri-oinarrizkoa da bi behaketa-espazioren arteko erlazioa (edo erlaziorik eza) bilatzeko bidea.
Datuak aztertzea, beraz, aldez aurretiko (egiturak) eta datu-bilketaren ondorengo datuak (aldagaien banaketak) landuz erlazio berriak bilatzea da; batez ere, unibertso handien kasuan, dagozkien behaketa-espazioen arteko erlazio berriak bilatzea edo haien baterako aldagarritasunen nondik norakoak atzematea.
Estatistikaren azken zeregina da errealitateko arazo jakin baten aurrean informazioa azaltzea eta aurkeztea; hau da, aldez aurretik ezarritako eta azterketaren ondorioz aurkitutako erlazio garrantzitsuak modu mamitsu eta ulergarrian adieraztea. Noski, zeregin horretan kontuan hartzekoak dira estatistikak egitearen helburua eta estatistikak (informazioa) jasoko dituztenen ezagutza-maila.
Kontzeptu horiek guztiak errealitateko arazo bati aplikatu eta estatistikak sortzearren, estatistikak bideratzen duen tresneria zenbait motatakoa da: zenbakizko taulak, grafikoak (barra-diagrama, histograma, denbora-diagrama, sakabanatze-diagrama...), estatistikoak (zenbakizko informazio-adierazleak: batez besteko balioa, desbideratze estandarra, mediana, korrelazio-koefizientea...), ereduak (uniformea, normala, esponentziala...) eta eraldaketak edo transformazioak (birkodeketa, logaritmikoa...). Begien bistakoa denez, tresneria matematiko guztia geometriari, analisiari eta aljebrari dagokie gehienbat.
Estatistika hitza eta estatistika-motak
Orain arte azaldutako guztia estatistikari eta estatistikei dagokien jatorrizko ulerkera izan da, hau da, unibertso bateko objektuei egindako behaketetan gauzatzen den datu-biltzeari, -aztertzeari eta -mamitzeari buruzko ulerkera.
Jatorrizko ulerkera horren lehenengo aztarnak lehendabiziko zibilizazioetan aurkitu daitezke: egiptoarrek, txinatarrek, sumertarrek, grekoek, erromatarrek eta abarrek biztanle-, soldadu- eta ondasun-erroldak egiten zituzten jadanik. XVII. mendean egin ziren lehendabiziko taulak (hilkortasunari buruzkoak), eta aritmetika politiko izena zuen jakintza-arloa garatu zen. Ildo horren barruan kokatu behar da estatistika hitzaren jatorria. 1749an erabili zen lehendabizikoz statistik hitza alemanez, estatu baten gizarte-, politika- eta ekonomia-ezaugarriak adierazteko; antza denez, latineko statisticum collegium (“estatu-batzordea”) eta italierako statista (“politikari”) hitzetik eratorri zen. Horrez gero, datu-biltze eta -sailkatzeak sistematikoki egiten hasiak ziren, eta estatistika hitzaren esanahia zabaldu egin zen.
Areago, bada beste ulerkera bat XVIII. mendean hasi eta XIX. mendean erabat finkatu zena estatistika eta estatistiken esanahian. Behatutakoak unibertsoko (populazioko) objektu guztiak direnean, errolda deritzo, baina, guztiak ez direnean —ezinaz edo komenentziaz, gehienetan gertatu ohi den legez—, unibertsoaren lagin edo erakuskari batekoak izaten dira behatutakoak, eta horien bitartez aurkitutako informazioa (erlazio berriak) unibertso osora zabaldu nahi izaten da. Aipatutako aritmetika politikoan hasi ziren egiten nola-halako eragiketa biderkatzaileak zati batean behatutakoa populazio osora zabaltzeko.
Laginketaren kasuan, aintzat hartzekoa da laginetik laginera datuak aldatu egiten direla edo lagin batean bildutako datu-multzoa beste lagin askoren arteko bat besterik ez dela. Beraz, datu-multzoaren edo lortutako erlazioen ulerkera eta beste datuak edo lor zitezkeen erlazioen ulerkera alderatu behar dira. Lagina zoriz aukeratu baldin bada, laginean aurkitutako informazioen orokortze hori nolabait kontrola daiteke probabilitate-kalkulua erabiliz. Inferentzia (induktiboa) egiten da. Estatistikak orokortzeko datuetatik ondorioztatzeko garatu dituen metodoen multzoari inferitzeko estatistika deritzo (gure artean zabalduta dago inferentzia estatistiko terminoa, gazteleraren eta frantsesaren eraginez, baina kasu horretan estatistika hitza izenlaguna da). Horrela, metodo horietatik arestian aipatutakoak bereizteko, deskribatzeko estatistika erabiltzen du terminologia klasikoak (gure artean, estatistika deskribatzailea, eta, gaur egun, batez ere, datu-analisia).
Gurean, bi metodo-multzo horien izendapenak ez daude orekatuak, estatistika batean izena delako eta bestean izenlaguna, baina ingelesez (hortik hartuak dira termino hauek) bereizketa eta garrantzia orekatuta dago: descriptive statistics eta inferential statistics (bai, pluralean gainera).
Inferitzeko estatistikaren helburua, beraz, unibertsoaren irudikapen bat edukitzea da unibertsoaren lagin batean lortutako irudikapenaren bitartez. Inferitzeko estatistikaren gai nagusiak dira unibertsoari behatutako aldagaien ezaugarrien zenbatespena edo estimazioa eta aldagaien inguruan egindako hipotesi-proba edo hipotesi-alderaketa. Horien oinarrian, berriz, badira garrantzi handia duten beste bi gai: aipatutako laginketa eta saiakuntzen diseinua, aukeratutako objektuak aldagarritasunaren balizko eragile edo faktoreen menpean kontrolatuta egoteko burututako arloa.
Praktikan, datuek maiz izaten dute ziurgabetasun edo zorizkotasunen bat. Hori abiapuntutzat hartuz, estatistika matematiko deritzo (baita estatistika-teoria eta teoria estatistiko ere) datuetatik informazioa nola ateratzen den aztergai duen gaiaren oinarri teorikoak bilatu eta ikuspegi matematiko hutsetik (probabilitate-teoria, konbinatoria, aljebra, analisia eta matematikako zenbait alor baliatuz) aztertzen dituen jakintza-arloari. Inferitzeko estatistikaren ikuspegi teorikoa da, nolabait esateko. Ikuspegi horretatik, estatistikak matematikako beste alorren ondoan duen berezitasuna probabilitate-teoria da (neurriaren teoriaren kasu berezi bat). Estatistika deskribatzaileak, ikuspegi horretatik, ez du berezko oinarri matematikorik, ez baitu probabilitate-teoriaren beharrik.
Estatistika matematikoa besterik gabe, ordea, praktikatik urruti geratzen da, ez baita zilegi errealitateko datuei aldez aurretiko probabilitate-eredu bat ezarri eta, horren arabera, datuetatik ondorioztatzea, askotan egin ohi den legez. Izan ere, duela urte gutxi arte, ondorio estatistiko gehienak halako ereduetan oinarritzen ziren, batez ere eredu normalean (kanpaiaren itxura duen kurba), analitikoki oso propietate onak (kalkuluetarako sinpleak eta ulertzeko aproposak) ondorioztatzen zirelako. Bide horretatik, metodo estatistiko bat erabiltzea zilegi da, unibertsoak eta datuak biltzeko metodoaren betekizunak betetzen badira. Bestela, akats itzelak egin daitezke deskribatzeko eta interpretatzeko garaian, eta ondorioz hartutako erabakiak okerrak izan daitezke.
Probabilitate-ereduek egokitu behar dute datuetara, eta ez alderantziz. Beraz, praktikan, aztergai den problemak bestelako ondorioak eskatzen dituenean, estatistika deskribatzailea (datu-analisia) ezinbestekoa izateaz gain, inferitzeko estatistikaren aurretik kokatu beharra dago. Halako zeregina burutzeko, bide berri honetan garrantzi handia du konputazioaren eta konputagailuaren garapenak.