Hasieran, termodinamikaren zero legeari ez zitzaion garrantzi handirik eman; berehala antzeman zen, ordea, horrelako legea beharrezkoa zela termodinamikaren egitura logikoarentzat. XX. mendearen hasieran esleitu zitzaizkion ordena-zenbakia eta izena lege horri. Ordurako, lehen legea eta bigarrena erabat onartuak ziren, eta, beraz, ezin zen zenbatze-aldaketarik onartu. Argi uzten saiatuko garenez, legeek oinarri esperimental bana damaigute propietate termodinamiko bat definitzeko. Zero legeak tenperatura propietatea finkatzen du; seguruenera, propietateetan ezagunena da, baina, berebat, misteriotsuena.

Termodinamika, zientziaren beste zenbait diziplinen antzera, eguneroko bizitzan darabiltzagun terminoak erabiltzen eta fintzen ditu —zenbaiten arabera bahitzen ditu—, horrenbestez, terminoek esangura zehatza hartzen dute: artikulu osoan antzemango dugu hori. Hasi bezain pronto ikusiko dugu. Termodinamikan, sistema da aztertuko den unibertsoaren zatia. Sistema bat izan daiteke burdin zatia, ura duen prezipitatu-ontzia, motor bat edo giza gorputza. Are gehiago, aipatutako horien zati bat ere izan daiteke. Gainerako unibertsoari ingurune deritzo. Ingurunean gu geu gaude, sistema aztertzen eta sistemari buruzko ezaugarriak eta propietateak ondorioztatzen. Askotan, gehienetan ez bada, ingurunea da tenperatura konstantean dagoen ur-bainua: horixe da benetako ingurunearen hurbilketa kontrolagarria. Sistemak eta inguruneak, elkarrekin, unibertsoa osatzen dute. Gure aburuz, unibertsoa dena da; aldiz, termodinamika-aditu batek uretan (ingurunea) murgildutako prezipitatu-ontzia (sistema) unibertsotzat jo dezake.

Sistema bat haren mugek definitzen dute. Sistema bat irekia da materia sartu edo atera badezakegu. Zabalik dagoen termoa, esaterako, sistema irekia da: zabalik egonik bete eta hustu baitezakegu. Materiarekiko iragaztezina den mugadun sistemari itxi deritzo. Edozerekiko iragaztezina den mugadun sistemari isolatu deritzo; sistema itxia ez da aldatzen haren ingurunean edozer gertatuta ere. Zerraturik dagoen termoa (hutseko isolamenduduna), esaterako, sistema itxia da.

Sistema baten propietateak sistema bera dagoen egoerarekiko mendekoak dira. Adibidez, gas baten presioak hark betetzen duen bolumenarekiko mendekotasuna dauka; eta, bolumen-aldaketaren ondorioak antzeman ditzakegu sistemaren hormak malguak badira. “Horma malguak" esamoldeak honako hau adierazten du: sistema baten muga osoa finkoa da, horren zati batena —pistoiarena— izan ezik, horrek barrura eta kanpora egin baitezake. Erabil dezagun pistoia —sistema baten mugaren atal higikorra— ondoren azalduko den kontzeptu garrantzitsua definitzeko; kontzeptu horrek, gainera, tenperaturaren eta zero legearen misterioa aurkezteko balioko digu. Demagun bi sistema itxi dugula, bi tanga, erdialdean pistoi bana dutela. Pistoiak finkatu dira tangak ez-higikorrak direla ziurtatzeko.

Bi tanga, bakoitza bere pistoiarekin. Oreka mekanikoa argitzeko mekanismoa

Pistoiak lotuz hagaxka finkoa dugu; modu horretan, pistoi batek barrurantz eginez gero, bestea kanporantz higituko da. Pistoiak finko mantentzen dituzten giltzak askatuko ditugu. Ezkerreko pistoiak eskuinekoa sisteman barneratzen badu, ezkerreko presioa eskuinekoa baino handigoa zela ondoriozta dezakegu, presioa bera neurtu gabe. Eskuineko pistoiak, berriz, ezkerrekoa menderatzen badu, orduan, eskuineko presioa ezkerrekoa baino handigoa zela ondoriozta daiteke. Giltzak askatutakoan ezer gertatzen ez bada, sistemen presioak berdinak zirela esan beharko genuke, presioaren balioa edozein izanik ere. Presioak berdinak direnean, oreka mekanikoa dugula esango dugu, teknikoki.

Alda dezagun mekanikatik termodinamikara, eta pasa gaitezen zero legearen mundura. Demagun A sistemaren hormak metalezko horma higiezinak direla; berebat, B sistemarenak. A eta B sistemak elkar ukitzen dutela jarritakoan aldaketa fisikoren bat gerta zitekeen bietan. Esaterako, haien presioa alda daiteke, edo bataren edo bien kolorea alda daiteke. Eguneroko hizkuntzan adierazita, batetik bestera beroa pasatu dela esango genuke, eta horren ondorioz, haien propietateak aldatzen dira. Dena dela, ez pentsa dakigunik beroa zer den: misterio hori da zero legearen beste aurpegi bat.

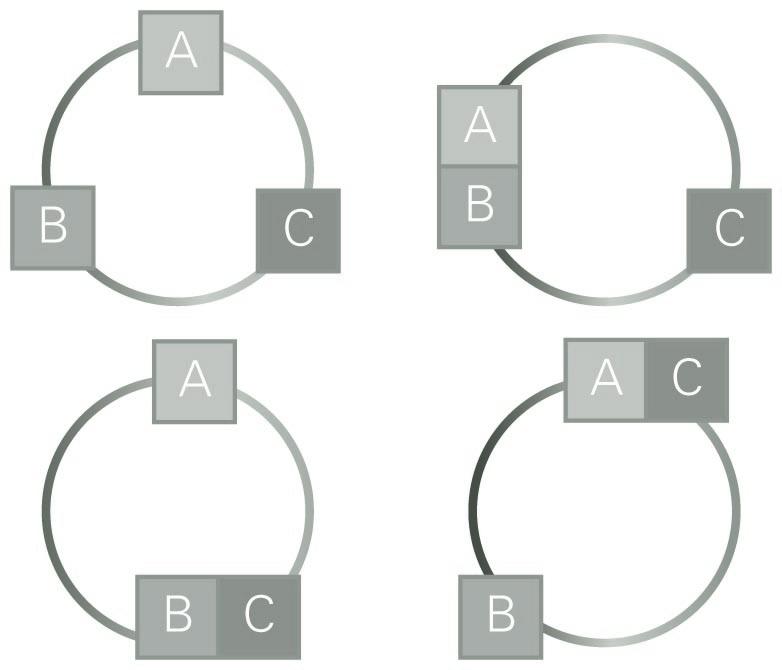
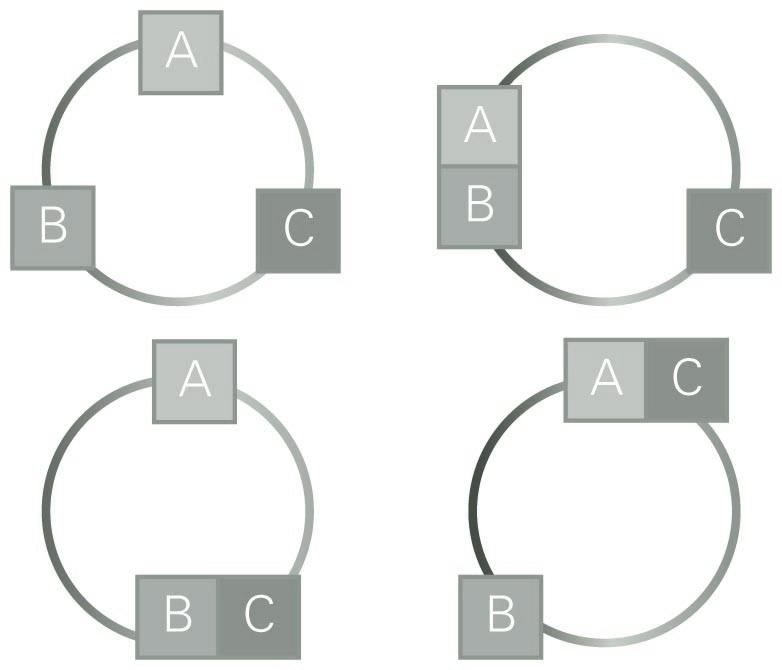
Oreka mekanikoaren beste ezaugarri bat behar dugu; azalekoa dirudi, baina tenperaturaren kontzeptua aurkitzea ahalbidetzen digu. Demagun A eta B sistemak oreka mekanikoan daudela ukipenean jarri eta giltza askatutakoan; hots, demagun presio berean daudela sistemak. Demagun, orain, bi sistema horien arteko ukipena eteten dugula eta A sistema hirugarren sistema batekin, C sistemarekin, pistoi baten bidez ukipenean jartzen dugula. Onar dezagun ez dela inolako aldaketarik antzeman; orduan, bi sistemak, A eta C, oreka mekanikoan daude, eta bien presioa berdina da, hortaz. Berebat, demagun A eta C-ren arteko ukipena eteten dugula eta C sistema B-rekin ukipenenean jartzen dugula. Saiakuntza bera egin gabe badakigu zer gertatuko den: ezer ere ez. A eta B sistemak presio berean daudenez, eta A eta C sistemak ere bai, ziur gaude C eta B sistemak presio berean egongo direla; gainera, modu berean, presioa oreka mekanikoaren adierazle unibertsala dela esan dezakegu.

Baina, era berean baita, gerta zitekeen aldaketa fisikorik gertatu ez izatea aurreko bi sistemak elkarren arteko ukipenean jarritakoan, nahiz eta biek metalezko hormak izan. Horrela bada, sistema biak elkarren arteko oreka termikoan daudela esaten da. Azter ditzagun orain hiru sistema, oreka mekanikoaz aritu garenean egin dugun moduan. Honako hau antzeman daiteke: A eta B ukipenean jartzen badira, eta oreka termikoan badaude, eta B eta C oreka termikoan jartzen badira, orduan, A eta C ukipenean jartzen direnean oreka termikoan egongo dira. Horixe da termodinamikaren zero legearen edukia:

A sistema B sistemarekin oreka termikoan badago, eta B sistema C-rekin, orduan, A eta B sistemak oreka termikoan daude.

Ikusi dugunez, presioak, propietate fisikoak berak, sistemak elkar ukitzen dutela jarritakoan, oreka mekanikoan egongo diren edo ez aurresateko ahalbidetzen gaitu, haien konposizioa eta tamaina edozein izanik ere. Berebat, zero legearen arabera propietate fisikoa existitzen da, zeinaren arabera sistemak elkarren arteko oreka termikoan egongo diren esango dugun, haien konposizioa eta tamaina kontuan hartu gabe. Propietate unibertsal horri tenperatura deritzo. Orduan, hiru sistemen arteko orekaren enuntziatua honako era honetan labur daiteke: hiru sistemak tenperatura berean daude.

Zero legea adierazteko eskema

Tenperatura: interpretazio estatistikoa

XIX. mendearen bukaera aldera, zientzialari gehienek atomoak benetan existitzen zirela onartu zutenean, eta kontatze-tresna huts baino ez zirela onartu zutenean, sortu zen Termodinamika Estatistikoa izeneko termodinamikaren atala. Horren helburua da materiaren propietate makroskopikoak lortzea, baina materia osatzen duten atomoetatik abiatuz. Atomoen portaera indibidualaz jabetzea baino milaka atomoen batez besteko portaeraz jabetzea beharrezkoagoa izatea da "estatistiko" izenlaguna erabiltzearen zergatia. Esaterako, gas batek eragiten duen presioaren jatorria da haren molekulek gasa dagoen tangaren hormetan egiten dituzten talkak; baina, presioa ulertzeko eta kalkulatzeko ez dugu kontuan hartu behar molekulek eurek egiten duten ekarpen indibiduala, baizik eta milaka molekulez osatutako multzoek tangaren hormen kontra talka egitean eragiten duten batez besteko efektua aztertu behar dugu. Laburbilduz, dinamika gorputz bakar baten portaeraz arduratzen da, termodinamikak, bere aldetik, sistema askoz osatutako multzoak aztertzen ditu.

Termodinamika estatistikoaren kontzeptu nagusia da Ludwig Boltzmannek (1844-1906), XIX. mendearen bukaera aldean, ondorioztatu zuen adierazpen bat. Ikusi dugu bada zero legeak tenperatura definitu duela, propietate makroskopikoen ikuspuntutik; berebat, Boltzmannek aurkitutako adierazpenak tenperatura kontzeptua definitzen du, atomoen ikuspegia erabiliz, eta, kontzeptua bera argitu ere argitzen du.

Boltzmannen adierazpenaren izaera ulertzeko, honako hau jakin behar dugu: atomo batek energia-maila jakin bat baino ezin du izan. Emaitza hori mekanika kuantikoari dagokio; diziplina horretatik ez dugu besterik behar, hori jakinda nahikoa dugu. Tenperatura jakin batean —ikuspegi makroskopikoa erabiliz—, atomoz osatutako multzo batean, batzuek dute izan dezaketen energiarik txikiena (“oinarrizko egoeran" daudela esaten da); beste batzuk posible den hurrengo energia-mailan daude, beste batzuk energiaren hurrenkeran hurrengo mailan daude eta abar. Energiaren balioak gora egin ahala, energia-mailen populazioak geroz eta txikiagoak dira. Populazio horiek oreka-egoeraren balioak dituztenean, eta nahiz eta atomoak energia-maila batetik beste batera aldatu, energia-mailen populazioak ez dira aldatzen, batez beste. Gainera, balio horiek kalkula daitezke parametro bakarra erabilita, beta, behin egoeren energiak ezagunak izanda.

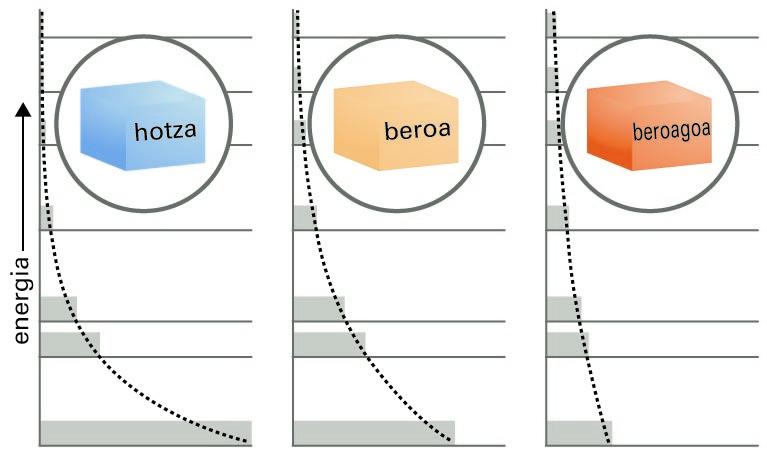
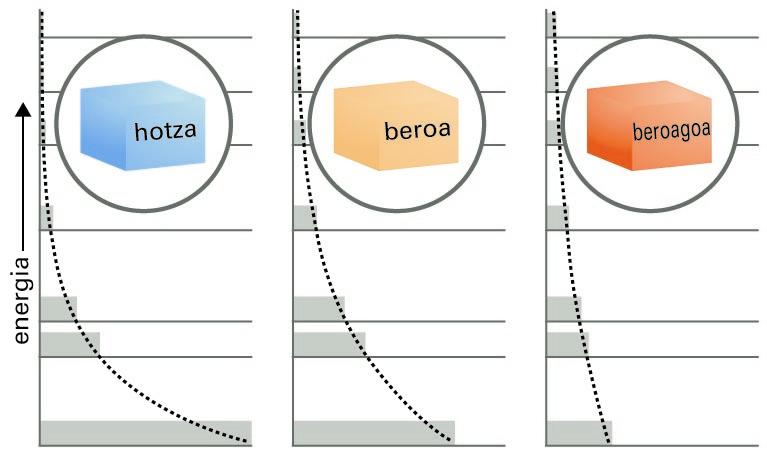
Arazoari aurre egiteko beste modu bat honako hau da: horman, altuera ezberdinetan kokatutako apalak ditugu, eta apalek adierazten dituzte energiaren egoera baimenduak, eta haien altuerek, energia-balio baimenduak. Berdin dio zer den energia horien jatorria; adibidez, izan daiteke molekulen translazio-higidura, biraketakoa eta bibrazio-higidura. Demagun pilota batzuk (molekula adierazleak) apaletara botatzen direla, eta ohart gaitezen geratzen diren tokiez. Honako hau antzemango dugu: energia berbera duten jaurtiketa askotan probableena den populazio-banaketa (apal bakoitzean geratzen diren pilota-kopurua) parametro bakarra erabiliz adieraz daiteke.

Boltzmannen banaketaren adierazpide grafikoa

Energia-maila baimenduen araberako molekula-banaketari, apaletan dagoen pilota-kopuru zehatzari Boltzmannen banaketa deritzo. Banaketa hori oso-oso garrantzitsua da, eta haren eitea ezagutzea merezi du. Gauzak errazteko, E energia-mailako populazioaren eta E0 txikienaren energia-mailako populazioaren arteko zatiduraren bidez emango dugu. Honako hau:

E energia-mailako populazioa

E0 energia-mailako populazioa = e-beta E

Argi dago, beraz, egoeren populazioek behera egiten dutela era esponentzialean, haien energiak gora egiten duen heinean: apal altuenetako pilota-kopurua baxuenetako kopurua baino txikiagoa da. Berebat, agerian da, beta parametroa zenbat eta txikiagoa izan hainbat eta txikiagoa dela energia-maila jakineko populazio erlatiboa; pilotak apal baxuetan pilatzen dira. Banaketa esponentzialak segitzen du, maila handietan pilota gutxiago izanik, gainera, populazioak geroz eta azkarrago beheratzen dira energia handietan.

Molekulez osatutako multzo baten propietateak kalkulatzeko, esaterako, gas batek egiten duen presioa, Boltzmannen banaketa erabiltzen denean, beta parametroa tenperaturaren (absolutua) alderantzizkoarekin identifika daiteke. Izan ere, hauxe da lotura: beta = 1/k T. Adierazpen horretan k da oinarrizko konstantea, Boltzmannen konstantea. k konstantearen balioa da 1,38 10 J × K; modu horretan beta Kelvin tenperatura-eskalari dagokio. Beta parametroa tenperaturaren alderantzizkoarekiko proportzionala denez, hauxe da inportantea: tenperatura handitzen denean beta txikitzen da, eta alderantziz.

Boltzmannen banaketaren garrantzi izugarria honako honetan datza: tenperaturaren esangura molekularra finkatzen du; beraz, molekulez osatutako populazioen banaketarik probableena adierazten duen parametroa da tenperatura. Energia jouletan neurtzen da (gizakion bihotz-taupadek 1 J bana kontsumitzen dute, gutxi gorabehera). Tenperatura handia denean (beta txikia), egoera anitzek dituzte populazio handiak; tenperatura txikia denean (beta handia), energia txikieneko egoerarengandik gertuko egoerek baino ez dute populazio esanguratsua. Populazioen tamaina edozein izanik ere, populazioek beti segitzen diote Boltzmannen formularen antzekoa den adierazpen esponentzialari. Apaletako piloten irudikoaren arabera, tenperatura txikiak (beta handia) indar txikiko jaurtiketei dagozkie, eta horietan pilotak apal baxuetara baino ez dira ailegatzen. Tenperatura handiak (beta txikia) indar handiko jaurtiketei dagozkie, horrela, pilotak apal altuetara ere hel daitezke, eta, ondorioz, azken horietan populazio esanguratsuak ere egon daitezke. Hots, tenperaturak, parametro bakarrak, energia-egoeren populazio erlatiboei buruzko informazioa dauka, sistema orekan dagoenean.

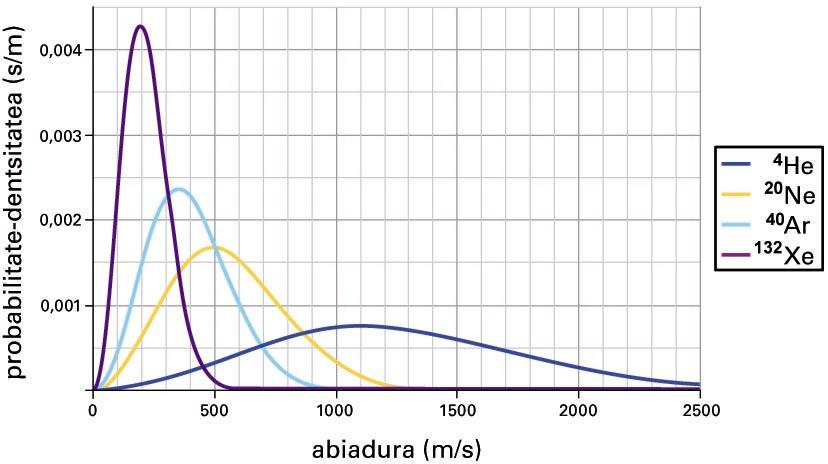
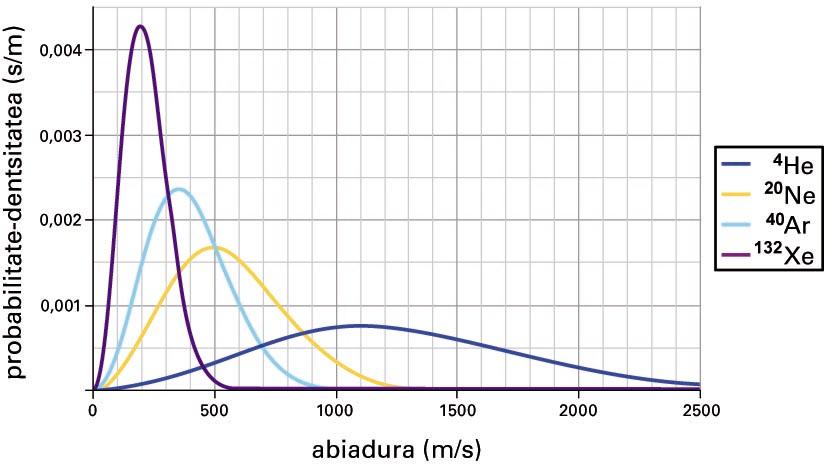
Atal honekin bukatzeko iruzkin positibo bat. Esandakoaren arabera, energia-egoera posibleen artean sistema baten molekulen orekako banaketa finkatzen duen parametroa da tenperatura, eta, zehatzago, beta. Imajina daitekeen sistema errazenetako bat, testuinguru horretan, gas perfektua (gas ideala) da. Horretan, molekulek talde kaotiko handi (izugarri handi) bat osatzen dute: horietan, batzuk azkar higitzen dira, beste batzuk motel, denak lerro zuzenean higitzen dira, abiadura desberdinetan, elkar joka; eta gasa kokatuta dagoen tangaren hormen kontra talka eginez, azken finean, presiotzat jotzen duguna sortuz. Izan ere, gasa da molekulez osatutako multzo kaotikoa (gas eta kaos hitzek jatorri berbera dute): kaosa bi mailatan ageri da, banaketa espazialari dagokionez eta molekulen abiadura-banaketari dagokionez. Energia zinetiko jakin bat abiadura bati dagokio, eta Boltzmannen banaketa erabil daiteke abiadura-banaketa adierazteko; horretarako, molekulak posibleak diren translazio-egoeretan banatu behar dira, ondoren, abiadura-banaketa hori tenperaturarekin erlazionatu behar da. Lortutako banaketari Maxwellen eta Boltzmannen abiadura-banaketa deritzo. James Clerk Maxwellek (1831-1879) ondorioztatu zuen lehen aldiz, nahiz eta beste modu batean.

Maxwellen eta Boltzmannen abiadura-banaketa

Kalkulua egiten denean, honako hau aurkitzen da: molekulen batez besteko abiadura tenperatura absolutuaren karratuarekiko proportzionala da: sistema epel batean (25 °C-an, 298 K-ean) airearen molekulen batez besteko abiadura % 4 handiagoa da eguna hotza (0 °C, 273 K) denean baino. Orduan, gas baten molekulen batez besteko abiaduraren neurritzat jo dezakegu tenperatura: tenperatura handiak batez besteko abiadura handiekin lotzen ditugu, eta, tenperatura txikiak, txikiekin.

Kanpotik, ingurunean kokaturik dagoen behatzaile baten arabera, tenperatura propietate bat da, eta propietate horrek esango digu horma diatermikoz elkarren arteko ukipenean jarritako sistemak oreka termikoan diren edo ez. Baiezkoan, tenperatura berean daude, eta ez da egoera-aldaketarik gertatzen; aldiz, egoera-aldaketa gertatzen bada, ez daude tenperatura berean; gainera, egoera-aldaketak aurrera egingo du tenperaturak berdindu arte. Barrutik, barnean dagoen behatzaile baten ikuspuntutik, ikuspen mikroskopiodun eta posibleak diren energia-egoeretan molekulen banaketak antzeman ditzakeen behatzailearen arabera, tenperatura da energia-mailen populazioekin loturik dagoen parametro bakarra. Tenperaturak gora egin ahala, aipatutako behatzaile horrek populazioen energia handiagorako desplazamendua antzematen du; aldiz, tenperaturak behera egiten duen heinean, populazioak energia txikiko egoeretara bueltatzen dira. Tenperatura jakin batean, egoera baten populazio erlatiboa txikitzen da energia-egoeraren energiarekin batera. Izan ere, tenperatura handitzen denean energia handiko energia-mailen populazioak gora egiteak esan nahi du geroz eta molekula gehiago bizkorrago higitzen (biraketak eta bibrazioak) direla, eta solido baten kasuan, haren atomoak geroz eta bibrazio handiagoak egiten dituztela haien batez besteko kokapenen inguruan. Agitazioa eta tenperatura eskutik doaz.