Puntu finko batetik zintzilik dagoen gorputz zurruna da pendulua, puntuaren inguruan aske oszila dezakeena. Lurraren grabitatea dela eta, oreka-posiziorantz azeleratuko duen berreskuratze-indar batek eragiten dio etengabe gorputzari. Hortaz, oreka-egoeratik aldentzen badugu, oszilatu egingo du gorputzak (haren higidura errepikatu egingo da, eta higidura periodikoa duela esango dugu).

Higidura periodiko hori dela eta, denbora neurtzearekin lotuta dauden tresnetan erabili ohi dira penduluak. Adibide adierazgarrienak pendulu-erlojua eta musikarako metronomoa ditugu.

Pendulu-motak

Zenbait motatako penduluak badaude ere, bi garrantzitsuenak bakarrik azalduko ditugu hemen.

Pendulu sinplea

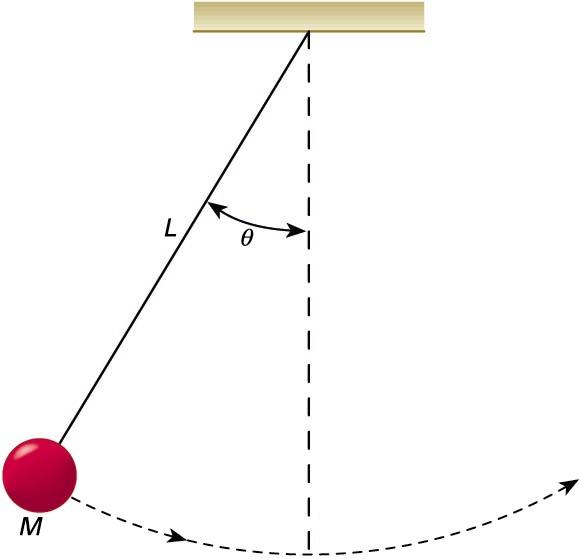
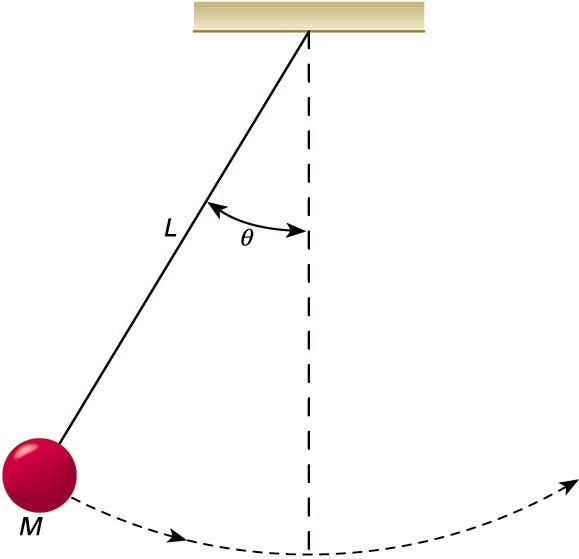
Pendulu-mota honetan, definizioko gorputz zurruna masa puntual bat da, eta hari masagabe batek lotzen du puntu finkora (ikusi hurrengo irudia). Idealizazio bat da, beraz, pendulu sinplea. Masaren oszilazio-angelua txikia bada, higidura harmoniko sinplea agertuko da. Halako higidura periodikoak ezaugarritzeko, bi parametro erabiltzen dira nagusiki: periodoa eta maiztasuna. Periodoa, definizioz, masak joan-etorri bat egiteko behar duen denbora da. Eta maiztasuna, berriz, penduluak denbora-unitatean egindako joan-etorrien kopurua da; agerikoa denez, elkarren alderantzizkoak dira bi parametroak.

Pendulu sinplearen higidura harmonikoan, higiduraren periodoa (T) ez da masaren balioaren araberakoa: hariaren luzeraren (L) eta grabitatearen azelerazioaren (g) mendean baino ez dago. Hona hemen periodoari dagokion adierazpen matematikoa:

$T=\text{2}\pi \sqrt{\frac{L}{g}}$

Pendulu sinplea

Pendulu sinplearen oszilazio-angelua txikia ez bada, beste adierazpen matematiko bat beharko dugu periodoaren berri izateko. Energiaren kontserbazioa erabiliz lortu daitekeen adierazpen hori honelako serie infinitu baten bitartez eman ohi da:

$T=\text{2}\pi \sqrt{\frac{L}{g}}\left(1+\frac{1}{4}{\text{sin}}^2\frac{{\theta }_{\text{max}}}{2}+\frac{9}{\text{64}}{\text{sin}}^4\frac{{\theta }_{\text{max}}}{2}+\text{.}\text{.}\text{.}\right)$

non θmax den masaren oszilazio-anplitudea (bertikalarekiko desbideratze-angelurik handiena).

Ohartu gaitezen oszilazio-angelua txikia denean sinuarekin loturiko adierazpen horretako gaiak baztertzeko modukoak izango direla, eta higidura harmoniko sinpleari dagokion adierazpena lortuko dugu.

Pendulu fisikoa

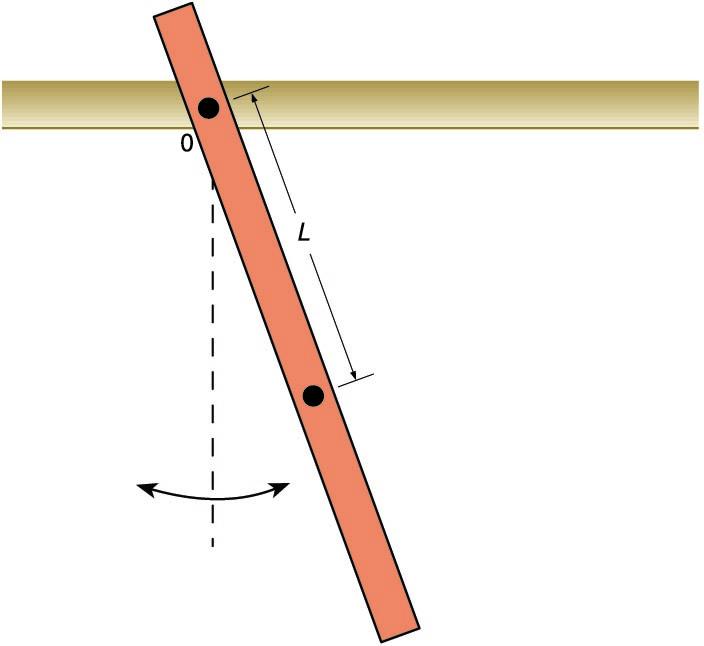
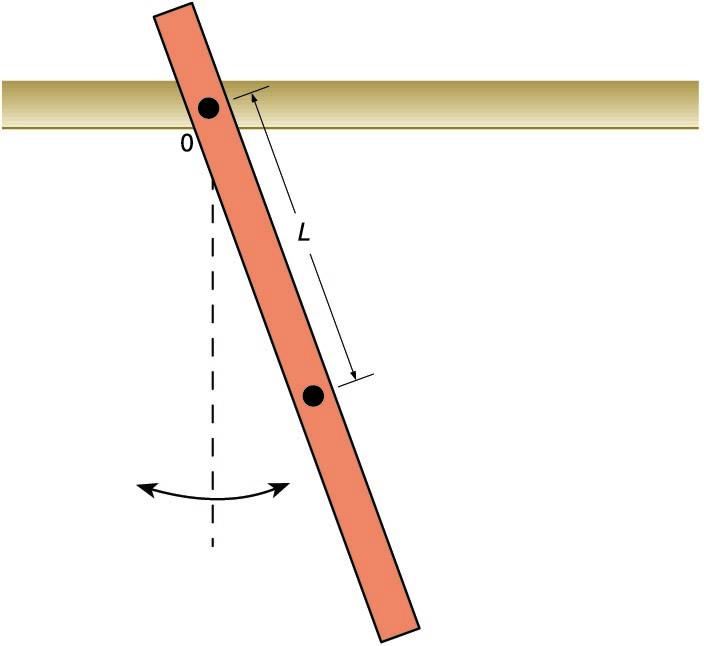
Pendulu sinplean, masa puntuala da, eta haria, masagabea; pendulu fisikoak, aldiz, kontuan hartzeko moduko tamaina eta masa ditu, eta, ondorioz, kontuan hartzeko moduko inertzia-momentua. Adibidez, metalezko hagaxka batek eratu dezake pendulu fisikoa (ikusi hurrengo irudia). Pendulu fisikoaren jokabidea pendulu sinpleak duen bera da, baina periodoarentzat beste adierazpen hau erabili behar dugu:

$T=\text{2}\pi \sqrt{\frac{I}{mgL}}$

I eta m, hurrenez hurren, hagaxkaren inertzia-momentua eta masa dira; L, bestalde, hagaxkaren masa-zentrotik puntu finkorainoko distantzia da.

Pendulu fisikoa