lente
- 1. Fis.
- sin. leiar
Azal biak edo bat (bestea laua da) kurbatuak dituen kristalezko edo bestelako material gardenezko disko-formako pieza, argi-izpiak era jakinean desbideratzen dituena eta hainbat tresna optikotan erabiltzen dena (irudiaren tamaina aldatzeko, adibidez).
1. Fis.
-

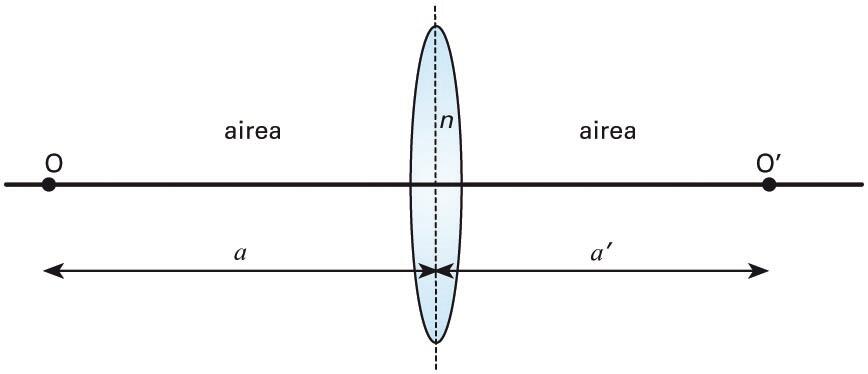
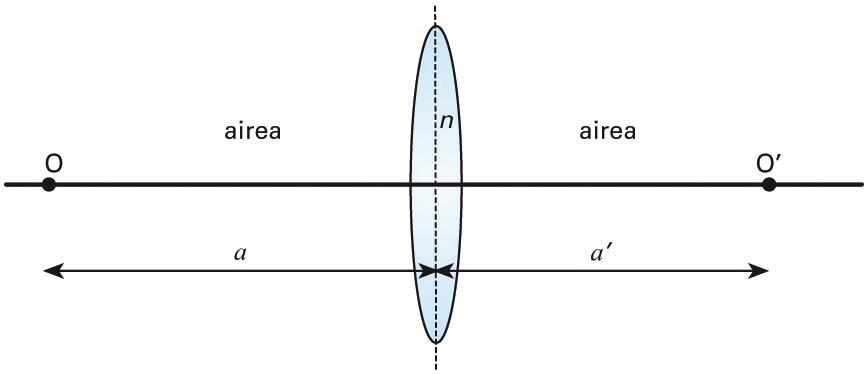
Leiar mehea. Errefrakzio-indizea n da. Objektuaren eta irudiaren posizioak a eta a' dira leiarrarekiko -
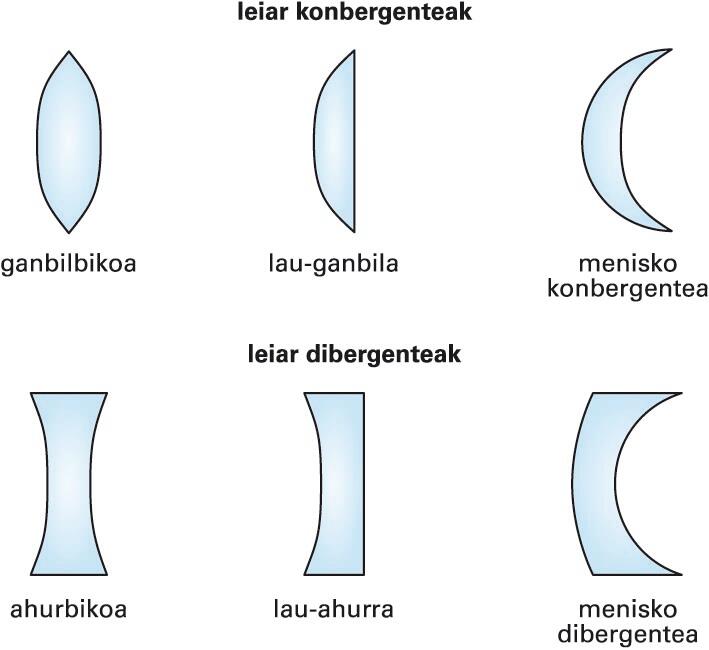
Leiar konbergentek eta dibergenteak -
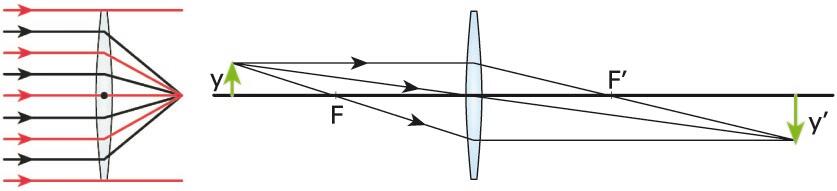
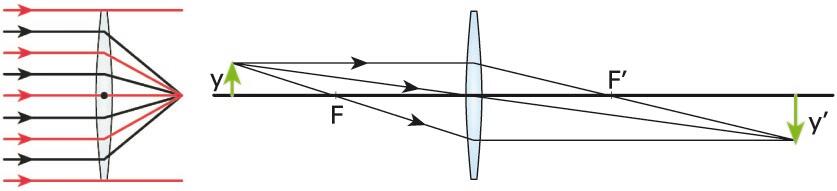
Irudien eraketa leiar konbergente batean. Adibide honetan, objektua eta irudia errealak dira; irudia alderantzizkoa da, eta objektua baino handiagoa -
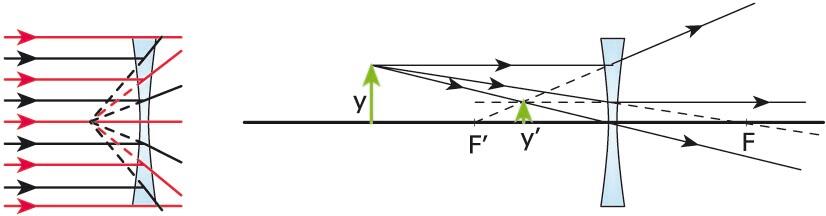
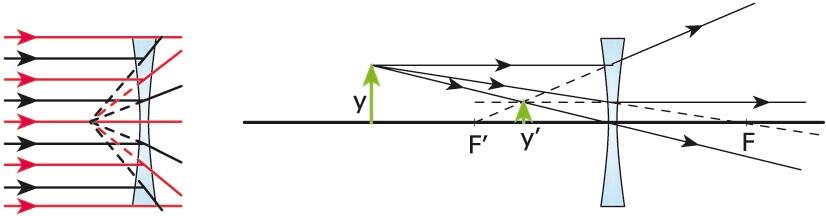
Irudien eraketa leiar dibergente batean. Kasu honetan, objektua erreala da, eta irudia, birtuala; irudia zuzena da, eta objektua baino txikiagoa
- 1. Fis.
- Azal biak edo bat (bestea laua da) kurbatuak dituen kristalezko edo bestelako material gardenezko disko-formako pieza, argi-izpiak era jakinean desbideratzen dituena eta hainbat tresna optikotan erabiltzen dena (irudiaren tamaina aldatzeko, adibidez).
Leiarra Edit
Egilea: Maria Jesus Elejalde
Leiarren oinarria errefrakzio izeneko fenomenoa da (errefrakzio). Argia konbergitu edo dibergitu egiten duten leiarrez gain, beste leiar-mota batzuk ere badaude, adibidez, leiar magnetikoak eta leiar grabitatorioak. Optikan, errefrakzio-indize desberdina duten bi ingurune gardenen arteko gainazal mugatzaileari dioptrio deritzo. Bi dioptrioz osatutako sistema optikoa leiarra da, hau da, leiarrak bi gainazal ditu; erabilienak beirazko xaflak dira. Dioptrio bien kurbadura-zentroak lerrokatuta daude, dioptrio bat esferikoa da, eta bestea laua edo esferikoa izan daiteke. Leiarrik orokorrenari leiar lodi deritzo. Leiar meheak, berriz, oso lodiera txikia du bere dioptrioen kurbadura-erradioekiko. Horrelako leiarrean, zentro optikoa defini daiteke. Leiar meheen ekuazioa bi dioptrioetako argiaren errefrakziotik ondoriozta daiteke.
Ekuazio hau erabili behar da leiar meheak ematen duen bukaerako irudia kalkulatu ahal izateko. Jo dezagun leiarra airean dagoela eta bere errefrakzio-indizea n dela (ikus hurrengo irudia). Objektuaren posizioa leiarrarekiko izango da, eta irudiaren bukaerako posizioa, . Bestalde, r1 eta r2 dioptrioen kurbadura-erradioak dira.
Leiar mehea. Errefrakzio-indizea n da. Objektuaren eta irudiaren posizioak eta dira leiarrarekiko
zatidura leiarraren ahalmen optikoa da. Hori dioptria izeneko unitatetan adierazten da, r1 eta r2 kurbadura-erradioak metrotan adierazten badira. Ahalmenaren alderantzizkoa distantzia bat da, leiarraren distantzia fokal deritzona, eta letraren bidez adierazten da. Objektua infinituan kokatuta dagoenean, leiarraren zentrotik distantziara, irudia fokuan eratzen da. Leiarraren albo-handipena, hots, irudiaren eta objektuaren tamainen arteko zatidura, hau da:
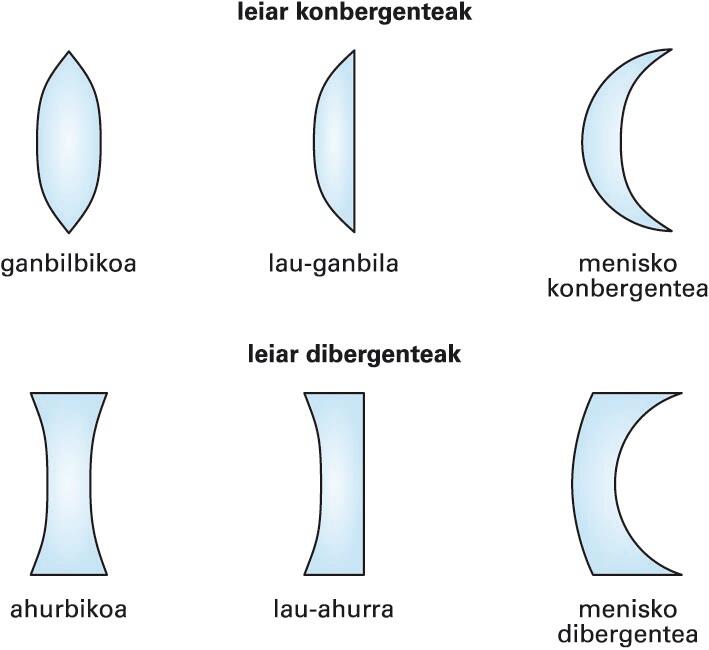
Dioptrioen kurbaduraren arabera, leiar konbergenteak edo hurbiltzaileak lodiagoak dira erdian ertzetan baino (ikus hurrengo irudia). Leiarra mugatzen duten bi dioptrioen arabera, ganbilbikoa, lau-ganbila edo menisko konbergentea izan daitezke. Leiar-mota horietakoak dira, adibidez, lupak. Leiar dibergente edo urruntzaileak lodiagoak dira ertzetan erdian baino. Leiarra mugatzen duten dioptrioen arabera, ahurbikoa, lau-ahurra edo menisko dibergentea izan daitezke. Mota horretakoak dira ateetako behatxuloak edo miopia zuzentzeko leiarrak.
Leiar konbergentek eta dibergenteak
Foku-distantzia positiboa denean , leiarrak konbergente edo hurbiltzaileak dira. Horiek eratzen duten irudia egiazkoa da, eta leiarraren zentroaren atzean eratzen da; aldiz, foku-distantzia negatiboa denean , leiarrak dibergente edo urruntzaileak dira. Sortutako irudia birtuala da, eta leiarraren zentroaren aurrean eratzen da.
Normalean, leiar konbergentea
![]() ikurraz adierazi ohi da; leiar dibergentea, berriz,
ikurraz adierazi ohi da; leiar dibergentea, berriz,
![]() ikurraz. Leiar konbergenteetan, ardatz nagusiaren paraleloak diren
izpiak (infinitutik datozen izpiak), sistema optikotik pasatu ostean, fokuan elkartu
egiten dira. Leiar dibergenteetan, aldiz, infinitutik datozen izpiak, leiarra zeharkatu
ostean, fokutik urrundu egiten dira. Bestalde, leiarraren zentrotik pasatzen diren izpiak
ez dira desbideratzen.
ikurraz. Leiar konbergenteetan, ardatz nagusiaren paraleloak diren
izpiak (infinitutik datozen izpiak), sistema optikotik pasatu ostean, fokuan elkartu
egiten dira. Leiar dibergenteetan, aldiz, infinitutik datozen izpiak, leiarra zeharkatu
ostean, fokutik urrundu egiten dira. Bestalde, leiarraren zentrotik pasatzen diren izpiak
ez dira desbideratzen.
Irudien eraketa leiar konbergente batean. Adibide honetan, objektua eta irudia errealak dira; irudia alderantzizkoa da, eta objektua baino handiagoa
Irudien eraketa leiar dibergente batean. Kasu honetan, objektua erreala da, eta irudia, birtuala; irudia zuzena da, eta objektua baino txikiagoa
Ikusmenaren akatsak zuzentzen dituzten betaurrekoak egiteko, leiarrez baliatzen gara. Leiarren eta ispiluen arteko konbinazioak teleskopio eta mikroskopioetan erabiltzen dira. Bi leiar konbergenterekin, Galileo Galilei fisikariak lehen teleskopio astronomikoa egin zuen.