entropia
- 1. Fis.
Sistema batean lana egiteko erabilgarri ez den energia-kantitatearen adierazgarri den funtzio termodinamikoa, sistemaren desordenarekin handitzen dena eta sistemaren energia-degradazioa ebaluatzea ahalbidetzen duena.
- 2. Inform.
Sistema baten desordenaren edo ausazkotasunaren adierazgarria den neurria. Datu-konpresioan, objektu batean dagoen datu ez-erredundante eta ez-konprimagarrien kopurua adierazten du (hau da, antzekoak ez diren datuen kopurua). Zifratzean, ostera, eransten den desordenaren eta ausazkotasunaren kopuruaren adierazgarria da. Softwarean, azkenik, programa behin eta berriro aldatzen denean sortzen den desordenaren eta nahaspilaren neurria ematen du.
1. Fis.
-

Sadi Carnotek bere lanean proposatutako motorraren eskema -
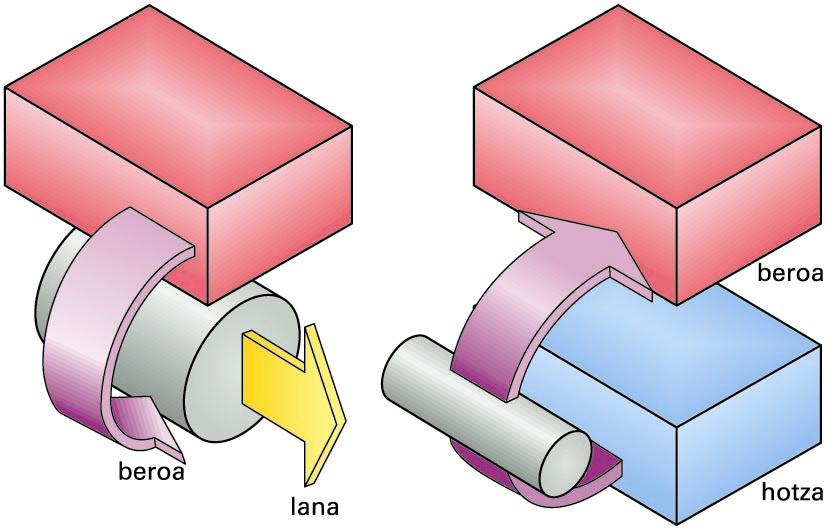
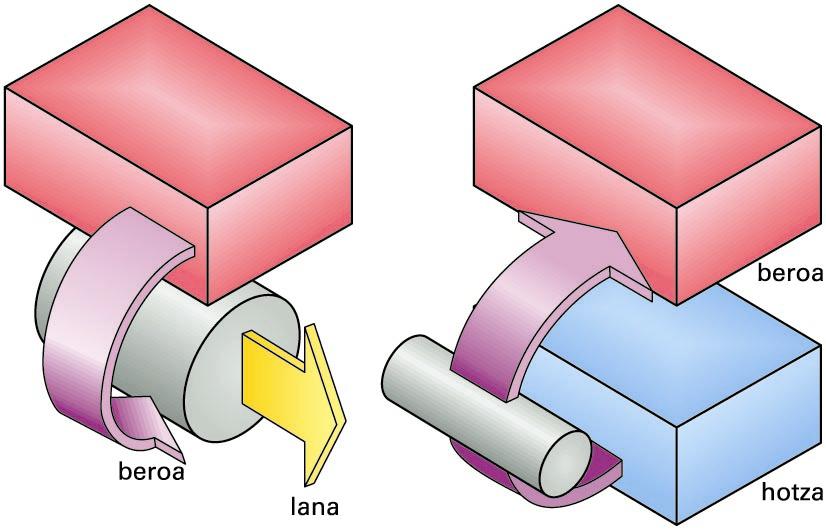
Kelvinek (ezkerrean) eta Clausiusek (eskuinean) egindako behaketak hauek dira, hurrenez hurren: bero-hustulekua (bero-iturri hotza) guztiz beharrezkoa da makina termikoaren funtzionamenduarentzat, eta beroa ez doa berez ... -
Kutxa batean sarturik ditugun partikulez osatutako sistemaren (gasaren eredua) entropiak gora egiten du, kutxa bera zabaltzean, kutxaren hormak elkarrengandik aldenduz baitoaz, eta ondorioz, partikulen energia-mailak ...
- 1. Fis.
- Sistema batean lana egiteko erabilgarri ez den energia-kantitatearen adierazgarri den funtzio termodinamikoa, sistemaren desordenarekin handitzen dena eta sistemaren energia-degradazioa ebaluatzea ahalbidetzen duena.
Entropia Edit
Egilea: Josu M. Igartua
Termodinamikaren bigarren printzipioak edo legeak, eta entropiak berak, garrantzi izugarria dute zientziaren osotasunean, eta, beraz, gizakiok dugun unibertsoaren ulertze arrazionalean: bigarren printzipioak eta entropiak edozein aldaketaren jatorriaz hornitzen gaituzte. Ez dute soilik motorren funtzionamendua edo erreakzio kimikoen gertatzea azaltzen; berebat azaltzen dute erreakzio kimikoen ondoriorik finenak: gizakion kulturaren sortze-ekintza literarioa, artistikoa eta musikala.
Termodinamikaren printzipio edo lege baten formulazioak eta interpretazioak sistemaren propietate bat dakar ondorioz: 0 printzipiotik T tenperatura sortzen da, eta U barne-energia, lehen printzipiotik. Era berean, bigarren printzipioaren ondorioa da beste propietate termodinamiko bat existitzen dela: entropia (S ikurraz adierazten da). Ideiak finkatzeko asmotan, esan dezagun ezen U barne-energiak sistema batek duen energia kantitatea adierazten duela, eta S entropia energia horren kalitatearen neurria dela: entropia handia kalitate txikia da; entropia txikia, aldiz, kalitate handia.
Zientziaren indarra abstrakziotik dator. Nahiz eta sistema zehatz baten behatze arretatsuak izadiaren ezaugarri bat azalera dezakeen, ezaugarri hori argituz, behatze hori era abstraktuan jarriz haren aplikazio-maila erabat heda daiteke. Bigarren printzipioa lurrun-makinaren behatzetik ondorioztatu zen, baina edozein aldaketari aplika dakioke, era abstraktuan adieraziz gero. Hots, lurrun-makinak aldaketaren funtsa barneratzen du; gizakion ekintza orok, digestiotik hasi eta sortze artistikoraino, lurrun-makinaren funtzionamenduaren oinarriak azaltzen ditu.
Lurrun-makina galdarak, balbulek, hodiek eta pistoiek osatzen dute. Baina makinaren funtsa errazagoa da; honako hauek osatzen dute: energia beroa duen iturria (tenperatura handian dagoen iturria edo bero-iturri beroa), beroa lan bihurtzen duen mekanismo bat —pistoia, turbina—, eta bero-hustulekua (edo bero-iturri hotza), azken horretatik erabili ez den energia desagerrarazten da, bero eran. Bero-iturri hotza zer den sumatzen beti ez da erraza, ingurunea bera izan baitaiteke, eta ez beren-beregi diseinatutako zerbait.
XIX. mendearen hasieran, Sadi Carnot ingeniari gazte frantsesak (1796-1832) Frantziaren botere ekonomikoa eta militarra bultzatu nahi zuen, eta horretarako lurrun-makinaren errendimenduaren murrizketak aztertu zituen. Garai hartan onartua zen ideiatik abiatu zen Carnot: beroa nolabaiteko jariakin ezin neurtuzkoa zen, berotik hotzera jariatzen zen, eta lana egiteko gai zen, gradientean behera, ur-errota higiarazten duen uraren antzera. Eredua ez zen zuzena, eta, halere, Carnotek emaitza zuzena eta harrigarria ondorioztatu zuen: lurrun-makina ideal baten errendimendua ez dago lan-substantziaren mende, baizik eta tenperaturen mende dago; beroa hartzen den bero-iturri beroaren tenperaturaren eta kanporatzen den bero-iturriaren tenperatura hotzaren mende, hain zuzen ere.
Sadi Carnotek bere lanean proposatutako motorraren eskema
Lurrun-makinaren errendimendua —makina termikoarena, oro har— honako era honetan definitzen da: ekoizten duen lanaren eta xurgatzen duen beroaren arteko zatidura da. Hortaz, bero osoa lan bihurtuko balitz, haren zatiren bat bera ere kanporatu gabe, orduan, errendimendua 1 litzateke. Carnotek honako adierazpen hau ondorioztatu zuen; adierazpena da Titurri bero eta Titurri hotz tenperatura absolutuen artean dabilen makinari dagokion errendimendu maximoa:
errendimendua = 1 - Titurri hotz / Titurri bero
Hain erraza den adierazpen hori termodinamikoki ideala den edozein makinari dagokio, eta ez da makinaren diseinuaren mendekoa. Adierazpen horrek errendimendu teoriko maximoa damaigu, eta nahiz eta esfortzu handiz makinaren diseinua hobetzen saiatu, ez dago hark finkatutako balioa gainditzerik. Esaterako, zentral elektriko baten turbinei 300 °C-an (573 K) dagoen lurrun gainberotua ematen bazaie, eta galtzen den beroa ingurunera, 20 °C-an dagoena (293 K), kanporatzen uzten bazaie, errendimendu maximoa 0,46 da; hortaz, erregailuak erretzen duen erregaitik sortzen den beroaren % 46 baino ezin da elektrizitate bihurtu; eta tenperatura horiek finkoak izanik, ez dago diseinurik errendimendua hobetuko duenik. Bihurtze-errendimendua hobetzeko bi modu dago: ingurugiroaren tenperatura txikitzea edo, osterantzean, tenperatura handiagoko lurruna ematea turbinei. Errendimendua % 100 izateko, ingurunearen tenperaturak nulua izan beharko luke (Titurri hotza = 0), edo lurrunaren tenperaturak infinitua (Titurri beroa = infinitu); bi horiek ezinezkoak dira.
Mendeak aurrera egin zuen, eta beroari buruzko ardura areagotu zen; bi erraldoi intelektualek aldaketa aztertu zuten, izan ere beste ikuspegi bat erabili zuten beroa lan bihurtzea aztertzeko.
Erraldoietan lehenak, William Thomsomek —Lord Kelvin (1824-1907)—, makina termikoen funtsezko egituraz hausnartu zuen: ikusezina ezinbestekotzat jo zuen, bero-iturri hotza —askotan ingurunea bera; diseinatu gabekoa, beraz— funtsezkoa zela aurkitu zuen; konturatu zen iturri hotzik gabe makinak ezin zuela funtzionatu. Zehatz dezagun; honako hau da Kelvinen termodinamikaren bigarren printzipioaren enuntziatua:
ez da existitzen prozesu ziklikorik, bero-iturri batetik xurgatutako beroa oso-osorik lan bihurtzen duenik.
Beste modu batean esateko, izadiak zerga ezartzen dio beroa lan bihurtze ko prozesuari: bero-iturri berotik lortzen den energiaren zati bat inguruneari bero moduan eman behar zaio. Bero-hustulekuak derrigorrean egon behar du, nahiz eta identifikatzen erraza izan ez, beti ez baita diseinatzen. Zentral elektrikoetako hozteko dorreak, zentzu horretan, beraz, garrantzitsuagoak dira haien funtzionamenduarentzat, turbina konplexuak edo erreaktore nuklear garestia baino.
Bigarren erraldoia Rudolf Clausius (1822-1888) izan zen. Horrek prozesu errazaz pentsatu zuen, tenperatura ezberdinetan dauden gorputzen arteko bero-fluxuaz, hain zuzen. Eguneroko fenomenoa identifikatu zuen: energia berez joaten da tenperatura handian dagoen gorputz batetik tenperatura txikian (txikiagoan) dagoen gorputz batera. Are gehiago, Clausius konturatu zen alderantzizko prozesua, gorputz hotz batetik gorputz bero baterako bero-transferentzia —hots, tenperatura txikian dagoen gorputz batetik tenperatura handian (handiagoan) dagoen gorputz baterakoa— ez dela berezkoa. Izadiko asimetria bat aurkitu zuen: energiak gorputz beroetatik gorputz hotzetara bero eran pasatzeko joera dauka; baina kontrako pasatzea ez da berezkoa. Agerikoa den baieztapen hori honako era honetan, termodinamikaren bigarren printzipioaren Clausiusen enuntziatuaz ezaguna den eran, birformulatu zuen:
beroa ez da transferitzen tenperatura txikian dagoen gorputz batetik tenperatura handiagoan dagoen beste gorputz batera, prozesu horrekin batera beste tokiren batean bestelako aldaketarik gertatzen ez bada behintzat.
Beroa transferitu daiteke “okerreko” (berezkoa ez den) noranzkoan, baina transferentzia hori lortzeko lana egin behar da. Esandako hori eguneroko bizitzan beha daiteke: hozkailuan sartuz, objektuak hoztu daitezke. Prozesu horretan objektuetatik beroa ateratzen da, eta epel(ago) dagoen ingurunean uzten da. Baina hori lortzeko, lana egin behar da: hozkailuak, jarduteko, elikadura-iturri bati konektatuta egon behar du; hots, oso urrun egon daitekeen zentral elektriko batean erretzen den erregaia da ingurunean gertatu beharreko azken aldaketa, hoztea, gertatzearen erantzule.
Kelvinek (ezkerrean) eta Clausiusek (eskuinean) egindako behaketak hauek dira, hurrenez hurren: bero-hustulekua (bero-iturri hotza) guztiz beharrezkoa da makina termikoaren funtzionamenduarentzat, eta beroa ez doa berez gorputz hotz batetik bero batera
Kelvinen eta Clausiusen enuntziatuak behaketen ondorio dira. Ez da inoiz eraiki bero-hustulekurik gabeko makina termikorik, nahiz eta askotan zer den sumatzerik ere ez dagoen. Berebat, inoiz ez da behatu gorputz bat bere inguruneko tenperatura baino tenperatura handiagora berez pasatzen.
Adierazi diren moduan enuntziatu horiek izadiaren legeak dira, behaketa orokorren ondorio baitira. Ba al da bigarren printzipiorik edo legerik? Zergatik ez da izendatu Kelvinen enuntziatua bigarren printzipio, eta Clausiusena, hirugarren printzipio?
Logikaren ikuspegitik, bi enuntziatuak baliokideak dira, bi enuntziatuek elkar inplikatzen dute. Praktikan, erabilgarria da bigarren legearen bi enuntziatu izatea; hau da, bi enuntziatuak bildu eta erraza den enuntziatua aurkitzea.
Hori lortzeko asmotan, Clausiusek egindako lanari erreparatu eta funtzio termodinamiko berria definituko dugu: S, entropia.
Clausiusek honako era honetan definitu zuen sistema baten entropia-aldaketa: bero eran transferitutako energia eta transferentzia hori gertatu den tenperatura absolutuaren arteko zatidura:
Entropia-aldaketa = era itzulgarrian transferitutako beroa / tenperatura
“Era itzulgarrian” baldintza garrantzitsua da: onartu behar da bero-trukea sistemaren eta ingurunearen arteko tenperatura-diferentzia infinitesimala dela eta gertatzen dela. Garrantzi handikoa da agitazio termikoko gune zurrunbilotsurik ez agertzea.
Arestian aipatu da entropia dela metaturik dagoen energiaren “kalitatearen" neurria; aurrera egiten dugun heinean “kalitatea" zer den argituko dugu. Lehenik eta behin, entropia eta desordena identifikatuko ditugu. Materia eta energia era desordenatuan banatzen badira, gas batean gertatzen den moduan, entropia handia da; materia eta energia era ordenatuan metatzen badira, aldiz, entropia txikia da; azken hori da kristal baten kasua. Desordenari buruzko ideia hori gogoan dugula, Clausiusen enuntziatuaren ondorioak aztertuko ditugu, eta baieztatuko dugu hark, entropia dela sistemaren desordenaren neurria, barnean hartzen duela.
Clausiusen entropia-aldaketaren definizioa argitzeko irudia honako hau izan daiteke: liburutegi batean edo kale jendetsuan barrena eztul egitea. Liburutegia da tenperatura txikian dagoen, agitazio termiko txikiko, sistemaren metafora; eztul egitea da bero erako energia transferitzea. Liburutegi isilean bat-batean eztul egitea oso aztoratzailea da; desordenak gora egiten du hein handi batean. Aldiz, beste muturrean, kale jendetsua da tenperatura handian dagoen, agitazio termiko handiko, sistemaren metafora; kale horretan eztul egite berberak desordena txikia eragingo du, entropia-aldaketa txikia, beraz. Argi dago bi kasuetan ondoriozta daitekeela entropia-aldaketak izan beharko lukeela tenperaturaren berreturaren batekiko (T-rekiko, esaterako), alderantziz proportzionala, entropia-aldaketa handiena tenperatura txikienean gertatzen baita. Bi kasuetan gehitutako desordena eztularen (bero eran transferitu den energia) proportzionala da, edo kantitate horren berreturaren batekikoa (lehena, kasu honetan). Clausiusen adierazpenak bat egiten du metafora honekin.
Termodinamikaren bigarren printzipioa entropiaren funtzioan adieraz dezakegu eta, berebat, froga dezakegu enuntziatu bakar batek Kelvinen eta Clausiusen enuntziatuak barnean hartzen dituela. Honako hau da aipatutako enuntziatu bakarra:
berezko aldaketa orok unibertsoaren entropia handitzen du.
Aurreko enuntziatuan gakoa unibertsoa hitza da; termodinamikan, unibertsoa sistema gehi ingurunea da. Ez da ezinezkoa sistemak edo inguruneak bakoitzak bere aldetik entropiaren beherapena izatea, tokiren batean beherapen hori konpentsatzen duen beste aldaketaren bat badago.
Zenbait prozesurekin lotutako entropia-aldaketa modu errazean aurresan badaiteke ere, entropia desordenaren neurritzat joz gero, aldaketaren zenbakizko balio erreala kalkulatzea ez da hain erraza. Esaterako, gas baten hedatze isotermikoak haren molekulak eta energia konstantea bolumen handiago batean banatzen ditu; beraz, sistema ez da hain ordenaturik egongo, hots, molekula jakin baten energia eta kokapena aurresateko, era arrakastatsuan, probabilitatea txikiagoa da; hortaz, entropiak gora egiten du.
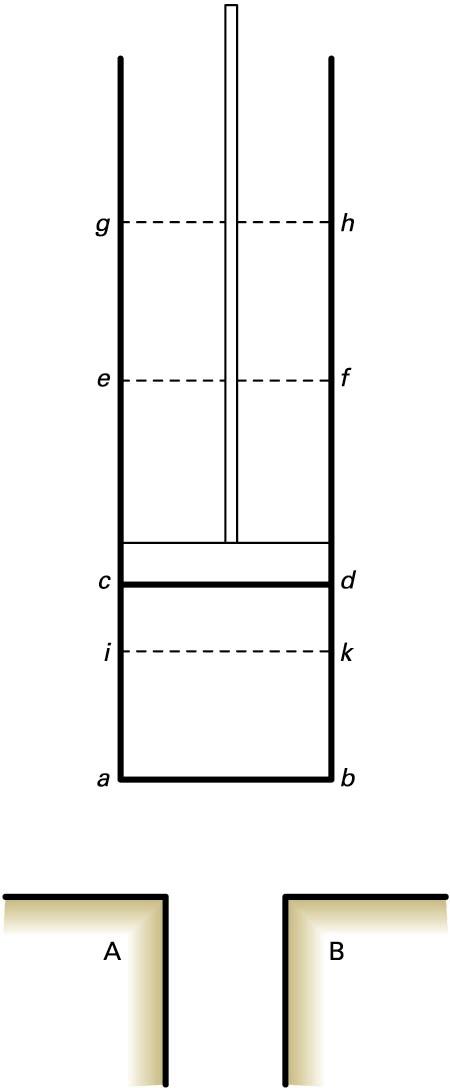
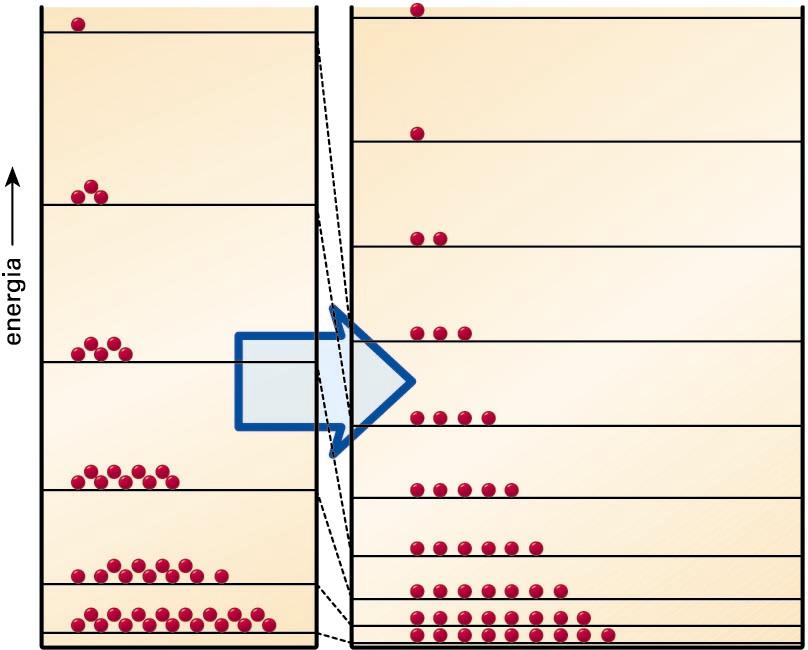
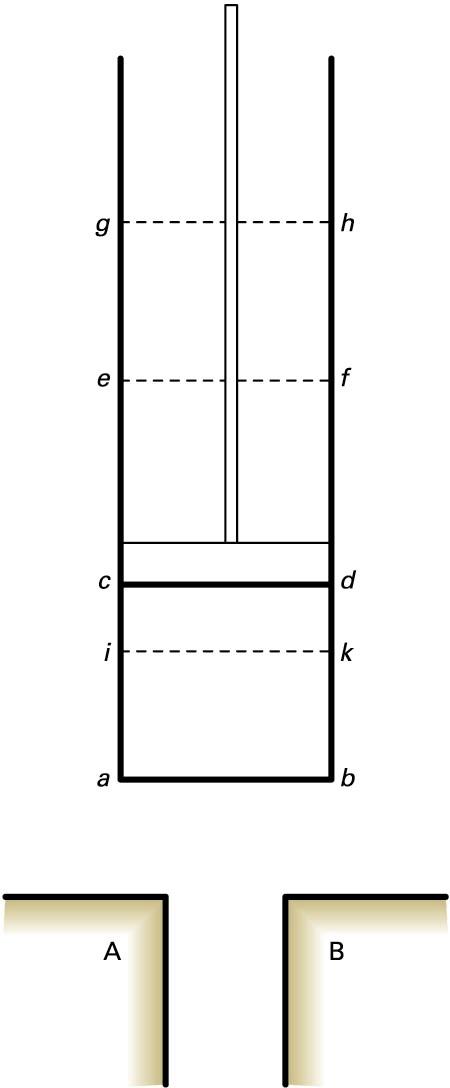
Korapilatsuagoa den era batean ere hel gaitezke emaitza berera. Era horrek “desordenaren" irudi egokia egiten du. Honako hau da: imajina ditzagun partikulak sailkatuta kutxa batean, konfinaturik dauden (sakonera infinituko potentzial-osina) partikulek dituzten energia-maila berezien arabera. Mekanika kuantikoaren bidez energia-maila posible horiek kalkula daitezke. Emaitza nagusia hauxe da: kutxako hormak zenbat eta aldenduago egon, hainbat eta gertuago egongo dira energia-mailak elkarrengandik. Giro-tenperaturan milaka milioi maila betetzen dituzte molekulek; molekulen banaketa da tenperatura horri dagokion Boltzmannen banaketa. Kutxa zabalduz doan heinean, Boltzmannen banaketak geroz eta maila gehiago barneratzen ditu eta, ondorioz, geroz eta zailagoa da aurresatea zein energia-maila dagokion zoriz hautatu den partikula bati. Molekulak betetzen duen energia-mailari lotutako ezjakintasun gero eta handiagoa da, hain zuzen, sistemaren “desordena”: horri entropia handiagoa dagokio.
Antzeko zerbait esan daiteke entropia-aldaketaz gas-lagin baten tenperaturak gora egindakoan. Clausiusen definizioan oinarrituriko termodinamika klasikoko kalkulu errazaren arabera, tenperaturak gora egiten duenean entropiak gora egin behar du. Gorakada hori erraz uler daiteke ikuspegi molekularra erabiliz. Bolumena konstante mantenduz, tenperaturak gora egiten badu, Boltzmannen banaketaren buztana luzatzen da, eta, beraz, energia-maila gehiago barneratzen ditu. Beste behin, hortaz, zorizko eran hautatutako molekularen energia-maila zein den esateko probabilitatea txikiagoa da, desordena handitzen da, eta, ondorioz, entropiak gora egiten du.
Hauxe da galdera, beraz: zer da entropiaren balioa zero absolutuan? Boltzmannen banaketaren arabera, T = 0 denean, zero absolutuan, sistemaren “oinarrizko egoera” (energiaren eskalan, lehen egoera, energiarik txikienekoa) baino ez dago beterik. Orduan, horren arabera ziur egon gaitezke ezen itsu-itsuan (zoriz) aukeratutako molekularen egoera oinarrizkoa izango dela; ez dago energia-banaketari buruzko ziurgabetasunik, eta, hortaz, entropia nulua da.
Ludwig Boltzmannek adierazpen erraz-erraza proposatu zuen sistema baten entropia absolutua adierazteko: S = k LnW.
Adierazpenean agertzen den k konstanteari Boltzmannek konstante deritzo. Nepertar funtzioaren zenbakiak (W) esangura sakona dauka: sistemaren energia osoa konstante mantenduz, “konfigurazio” (energia-banaketa) baten pisua adierazten du; hots, energia jakinerako, molekulen konfigurazio ezberdinen kopurua da. Adierazpen hori termodinamika klasikoa bera baino zailagoa da erabiltzen, izan ere, termodinamika estatistikoaren kontzeptua da. Esan dezagun Boltzamannen adierazpenak balio duela ez bakarrik entropia absolutua kalkulatzeko, baita edozein aldaketarekin lotutako entropia-aldaketa kalkulatzeko ere. Kasu denetan, jakina, entropia-aldaketen adierazpen denak bat datoz, zehatz-mehatz, Clausiusen definiziotik ondorioztatzen diren horiekin.
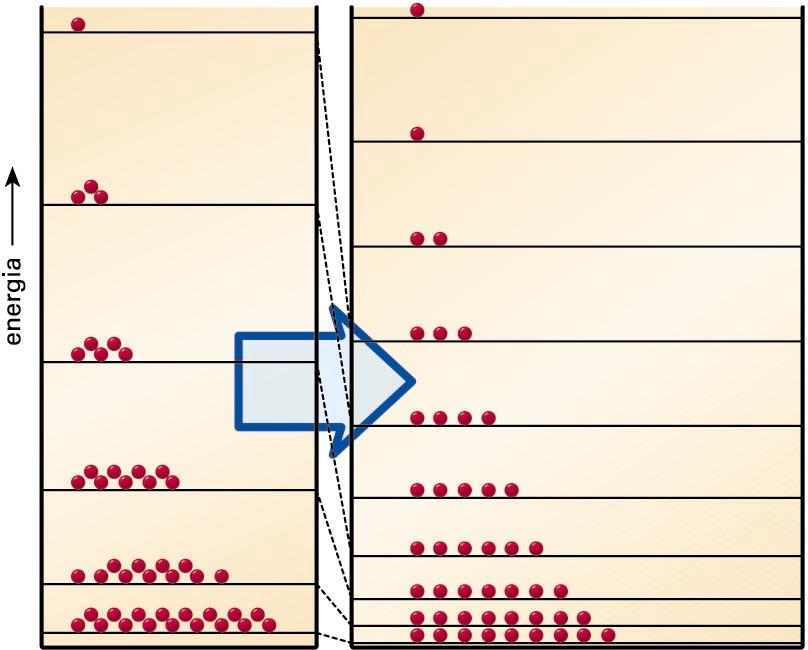
Kutxa batean sarturik ditugun partikulez osatutako sistemaren (gasaren eredua) entropiak gora egiten du, kutxa bera zabaltzean, kutxaren hormak elkarrengandik aldenduz baitoaz, eta ondorioz, partikulen energia-mailak elkarri hurreratzen baitira (hori guztia mekanika kuantikoaren bidez froga daiteke). Demagun tenperatura konstantea dela zabaltze-prozesu horretan, Boltzmannen banaketak energia-maila gehiago bereganatuko ditu, eta itsu-itsuan aukeratutako molekula bat energia-maila jakin batean egoteko probabilitateak behera egiten du. Hots, desordenak eta entropiak gora egiten dute gasak bolumen handigoa betetzen duenean
Artikuluaren hasieran esan dugu denok garela lurrun-makinak; izan ere, egia da lurrun-makinaren interpretazioak abstrakzio-maila nahikoa duenean. Desordenaren egituraren batek iraun dezan nahi izanez gero, beste tokiren batean desordena-maila handiagoa sortuz egin behar da, horrenbestez, unibertsoaren entropia-handitze netoa izango baita. Desordena hori gertatzen da aipatu dugun zentzu sofistikatuan. Hori guztia egia da, ikusi dugunez, benetako lurrun-makinaren kasuan. Baina, era unibertsalean ere bada egia. Esaterako, barne-errekuntzako motor batean erretzen den hidrokarburo likidoaren ordez, 2.000 aldiz gehiago betetzen duten gasen nahastea sortzen da (600 aldiz are handiagoa, erretzen den oxigenoa kontuan harturik). Are gehiago, errekuntzan askatzen den energia ingurunean barreiatzen da. Motorraren diseinuak desordenaren barreiatze hori bahitzen du eta eraikitzeko erabiltzen du, adibidez, gutxi ordenaturik dagoen zerbaitetik, adreilu-pilo batetik, egituraren bat, eraikuntza bat, sorrarazteko; edo korronte elektrikoa (elektroien fluxu ordenatua) zirkuitu batean zirkularazteko.
Erregaia janaria izan daiteke. Entropia handitzeari lotutako barreiatzea da jakien metabolismoa; hots, metabolismoaren ondoriozko energiaren eta materiaren barreiatzea. Barreiatze hori organismoaren bide biokimikoek aprobetxatzen dute, eta ez pistoiek eta engranajeek osatutako hurrenkera mekanikoak. Bide biokimikoek sortutako egitura aminoazidoetatik abiatuz eraikitako proteina izan daiteke. Jaten dugu, eta, ondorioz, hazten gara. Egituren izaerak ezberdinak izan daitezke; artelanak ere izan daitezke! Jatearen eta digestioaren ondorioz askatutako energiak sor dezakeen egituretako bat da zorizko jarduera neuronal eta elektrikotik eraikitako jarduera elektriko ordenatua. Jaten dugu, eta, ondorioz, sortzen dugu: artelanak, literatura-lanak eta ezagutza-lanak.
Lurrun-makinak, energia barreiatuz higidura ordenatua (lana) sortzen duen dispositiboa den heinean, gure organismoan gertatzen diren prozesu denak azaltzen ditu. Are gehiago, ortziko makina termikoa, eguzkia, eraikitze-iturrietan handienetakoa da. Denok bizi gara haren energiaren berezko barreiatzeari esker, eta, bizi garen heinean, gure ingurunean desordena sortzen dugu: ezin izango genuke bizi ingurunerik gabe. XVII. mendeko hausnarketa da John Donnek, jakin gabe bazen ere, Carnotek, Joulek, Kelvinek eta Clausiusek baino bi mende lehenago, aipatu zuen bigarren printzipioaren bertsioa: gizakiok ez gara uharteak.