Integrazioaren printzipioak Isaac Newton eta
Gottfried Leibniz matematikariek ezarri zituzten XVII. mendearen amaieran. Bi
problema hauek kontsideratzen baditugu:
-
funtzioa ezaguna izanik, kalkulatu beste funtzio bat, non bere deribatua
den. Deribatuaren alderantzizko eragiketa
izango da hori.
Bi problema
horien arteko erlazioa Isaac Newton eta Gottfried Leibniz matematikariek
frogaturiko Kalkuluaren Oinarrizko Teoreman ezartzen da. Integralak eta
deribatuak kalkuluaren oinarrizko tresna bihurtu ziren, eta haien aplikazioak
funtsezkoak izan dira zientzian eta ingeniaritzan. Azalerak, arkuen luzerak,
bolumenak, lana eta inertzia-momentuak kalkulatzeko, integral mugatuak
erabiltzen dira, eta deribatuaren alderantzizko eragiketa integral mugagabea
da.
Integral mugatua
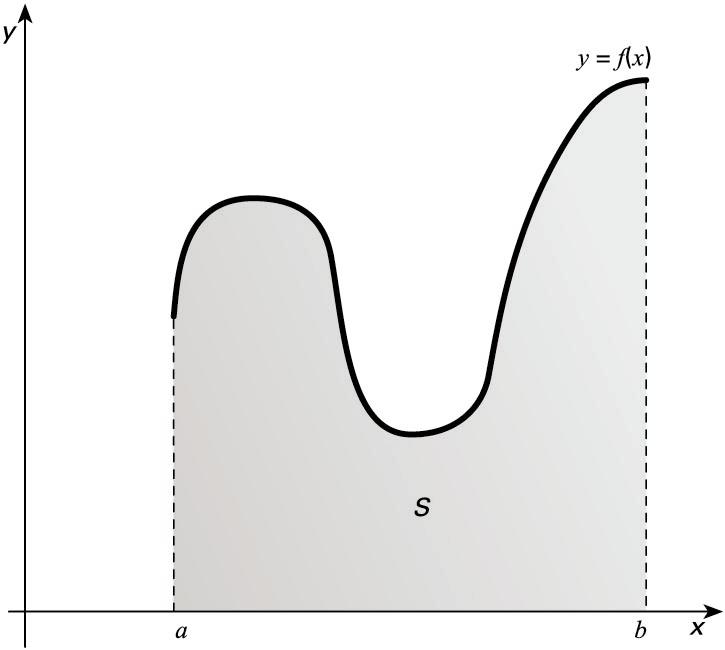
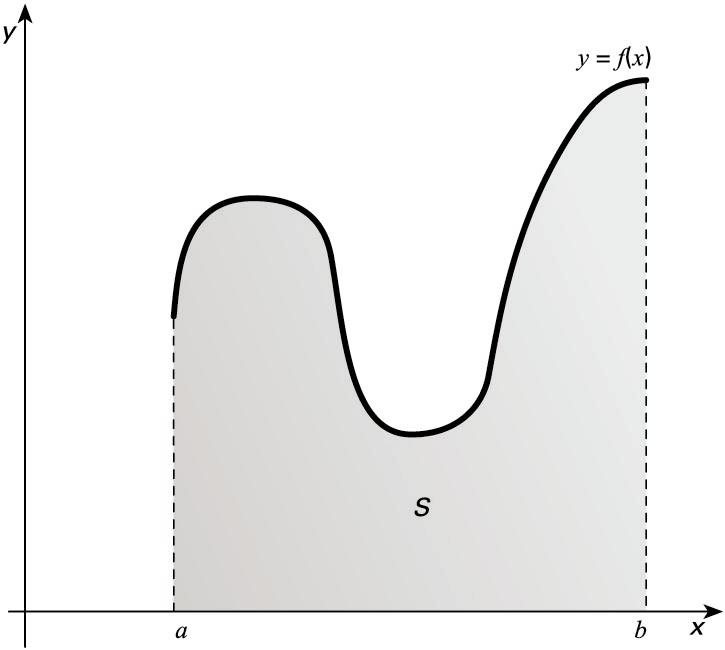
Kontsidera dezagun
tartean
jarraitua
eta positiboa
den
funtzioa,
zuzenek, ardatzak eta
kurbak mugaturiko eremuaren azalera
bada, -ren balioa -tik -rako integral mugatua izango da, eta ikur
honen bidez adierazten da:
=
.
Integral mugatua
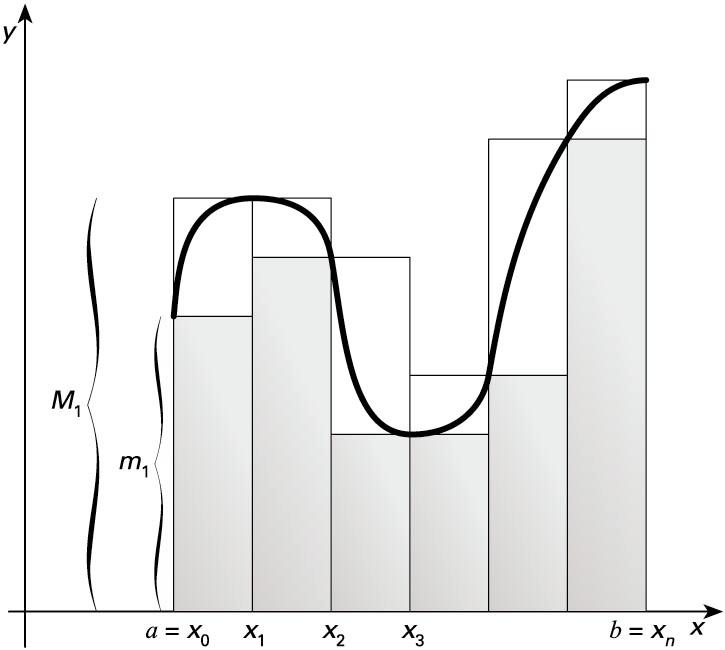
Integral mugatuaren definizio zehatza Bernhard Riemannek eman zuen. azalera kalkulatzeko, tartearen partiketa bat egiten da, ;
azpitarte bakoitzean funtzioaren balio
minimoa eta maximoa badira, altuera duen laukizuzena eta altuera duen laukizuzena kontsideratzen ditugu. laukizuzenen azaleren baturari
Riemannen
behe-batura
deritzo, eta, era berean, laukizuzenen azaleren baturari,
Riemannen
goi-batura.
Horrela, behe-batura = ; goi-batura = .
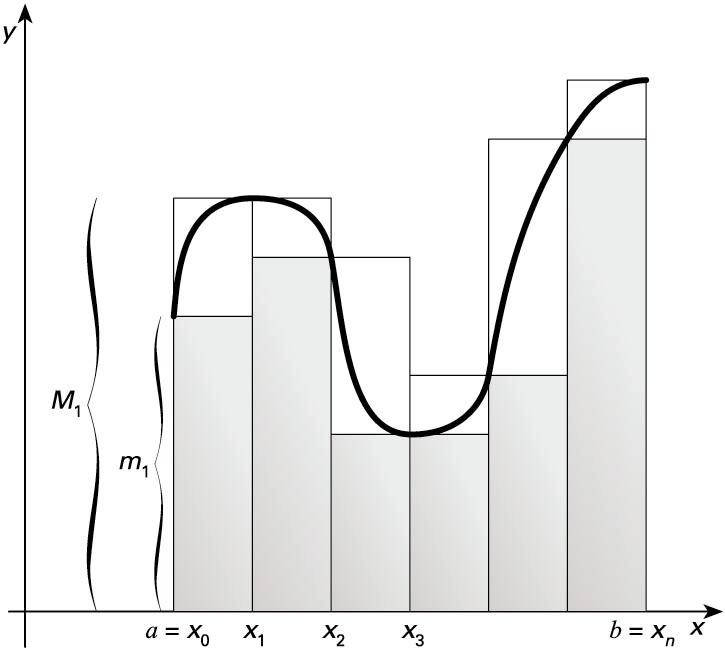
Goi-batura eta behe-batura
Riemannen baturak azaleraren hurbilketak dira. Behe-batura azalera baino txikiagoa da; goi-batura,
aldiz, baino handiagoa. Partiketaren puntu-kopurua
handituz, hurbilketa hobetzen da, eta, limitera pasatuz, Riemannen integral
mugatua definitzen da
Aurreko definizioan, izan behar du tartea definitzeko, baina integral mugatua denerako ere definitzen da:
,
eta kasurako, onartzen da dela.
XIX. mendearen hasieran, funtzioaren kontzeptua
orokortuz, beste integral-mota bat definitu zuen Henri Lebesgue matematikariak:
Lebesgueren integrala. Lebesgueren integrala Riemannen integralaren hedapena
da, eta oinarria izan da gaur egun erabiltzen diren beste integraletarako.
Integral mugagabea
Izan
bedi funtzioa, funtzioa existitzen bada, zeinetarako
egiaztatzen den, esango dugu funtzioa funtzioaren
jatorrizko funtzioa
dela. Horrela, integrazioa deribazioaren alderantzizkoa izango da.
baldin bada,
ere izango da eta, beraz, funtzio batek
jatorrizko funtzio anitz izango ditu; jatorrizko funtzio horiek formularen bidez adierazten dira, eta
funtzioaren integral mugagabe
deritzo.
Erabiltzen den ikurra hau da:
.
Integral mugatuen kalkulua
Kalkuluaren oinarrizko teoreman frogatzen da
deribazioa eta integrazioa alderantzizko eragiketak direla, eta teorema
horretatik ondorioztatzen da integral mugatuak kalkulatzeko erabiltzen den
Barrowen erregela:
funtzioa funtzioaren jatorrizko funtzioa baldin bada,
beraz
tarteko puntu guztietarako, orduan,
.
Adibidez, parabolak, eta zuzenek mugatzen duten eremuaren azalera integral mugatua da. funtzioaren deribatua denez, aurreko integral mugatua honela
kalkula daiteke:
.
Integralaren propietateak
Integral mugatuaren definizioa erabiliz
frogatzen dira propietate hauek:
-
Integrala eragiketa lineala da: eta konstanteak badira, orduan:
.
-
Azpitarteak: bada, orduan:
.
-
Funtzioen arteko desberdintzak:
bada tartean, orduan:
.