Naturan hainbat fenomeno aztertzerakoan, bi
magnituderen arteko erlazioa adierazteko beharra sortzen da. Adibidez, gorputz
baten egoera alda daiteke denboran zehar, edo gas baten presioa, baldintza
batzuetan, tenperaturaren menpekoa izaten da, edo gorputz bat erori eta lurrera
ailegatzean daraman abiadura altueraren menpekoa da. Fenomeno batean, kantitate
bat beste baten intentsitatearen ondorioa bada, sorturiko menpekotasuna funtzio
baten bidez deskribatzen da. Matematikan, funtzioaren kontzeptua bi
magnituderen arteko menpekotasuna adierazteko sortu zen; magnitude bat ezaguna
da (aldagai independentea edo funtzioaren “sarrera”), eta bestea, menpeko
magnitudea (menpeko aldagaia edo funtzioaren “irteera”).
Historia
Funtzioaren kontzeptuaren hastapenak XVIII.
mendearen hasieran kokatu behar dira. Newton eta Leibniz matematikariek garatu
zuten kalkulua ez zen funtzioen kalkulua. XVII. mendeko kalkuluan, oinarrizko
elementuak kurbak ziren; garai hartan, analisia kurbei buruzko problemak
ebazteko metodoen bilduma izan zen; kurbekiko ukitzaileak, azalerak eta kurben
luzerak aurkitzea izan zen lehentasunezko jarduera. Beraz, bi aldagairen arteko
erlazioa kurba baten bidez adierazten zen. XXVIII. mendearen lehenengo erdian,
analisia jatorrizko ikuspuntu geometrikotik urruntzen ari zen, eta formula
aljebraiko baten bidez definitzen zen funtzioa. Leonard Eulerrek 1748an
argitaraturiko
Introductio in Analysin Infinitorum
lanak eman zuen
funtzioaren lehenengo definizio zehatza: funtzio bat aldagai batez eta zenbaki
edo konstanteez osaturiko edozein adierazpen analitiko da. Baina Eulerrek
emandako definizioa funtzioak “onak” direnerako (jarraituak, deribagarriak eta
abar) bakarrik da baliagarria. 1720-1820 bitartean, matematikariek kalkuluko
tresna guztiak erabili zituzten funtsezko problema batzuen soluzioak
kalkulatzeko (adibidez, korda bibratzailearen problema eta beroaren problema).
Aipagarriak dira D’Alembert, Daniel Bernouilli eta Joseph Fourier
matematikarien garai hartako lanak. Planteaturiko problemen soluzioak nahiko
irregularrak ziren eta, beraz, funtzioaren definizio zehatzagoaren beharra
sortu zen. Gaur egun erabiltzen dugun funtzioaren definizioa Peter Dirichlet
matematikariak eman zuen.
Definizioa
Funtzioa adierazpen, erregela edo lege bat da,
non bi aldagai erlazionatzen diren, aldagai independentea eta menpeko aldagaia,
alegia.
Erregela bat existitzen bada zeinetarako
aldagaiaren balio bakoitzari
aldagaiaren balio bakar bat dagokion, esango dugu
dela
aldagai independentearen funtzioa. Bi aldagai horien arteko erlazioa
ikurraren bidez adierazten da. aldagaia
aldagai independentea
izango da, eta ,
menpeko aldagaia.
Funtzioa multzoko elementuetarako definitzen bada,
esango dugu funtzioaren
definizio-eremua
dela, eta, irudien multzoa ( elementuen multzoa)
bada, funtzioaren
irudi-multzoa
izango
da. Notazio hau erabiltzen da funtziorako: .
Funtzioaren definizio orokorrean, eta edozein multzo izan daitezke, baina adibide
arruntetan eta -ren elementuak zenbakiak izan ohi dira.
Aldagai independenteak hartzen dituen balioak
zenbaki errealak badira eta, beraz, definizio-eremua edo bere azpimultzoa bada, funtzioari
aldagai
errealeko funtzio
deritzo; irudi-multzoa ere denean,
aldagai errealeko funtzio erreala
izango da.
Zenbaki konplexuen multzoa
bada eta funtzioa
bada, aldagai konplexuzko
funtzio konplexua
izango da. Adibidez, elektrizitatean erabiltzen diren funtzioak funtzio
konplexuak dira.
Adibideak
Zirkulu baten azaleraren formulan,
A
azalera
r
erradioaren funtzioa da. Bi aldagai baino gehiagoko funtzioak oso arruntak dira
matematikan, adibidez, triangeluaren azaleran,
A=bh/2
,
A
azalera
b
oinarriaren eta
h
altueraren funtzioa da.
Zirkuluaren azaleraren formulan agertzen den
funtzioa
funtzio polinomiala
da. Funtzio polinomiala,
motakoa da, non koefizienteak ezagunak diren eta
x
edozein zenbaki
erreal den. Aldagai errealeko funtzio errealak modu geometrikoan adierazten
dira:
aldagai independentea ardatzean (lerro horizontalean) irudikatzen
da, eta menpeko aldagaia, ardatzean (lerro bertikalean). Horrela, koordenatuetako puntuek funtzioaren grafikoa
osatzen dute. Adibidez, funtzio polinomialaren grafikoa hau da:
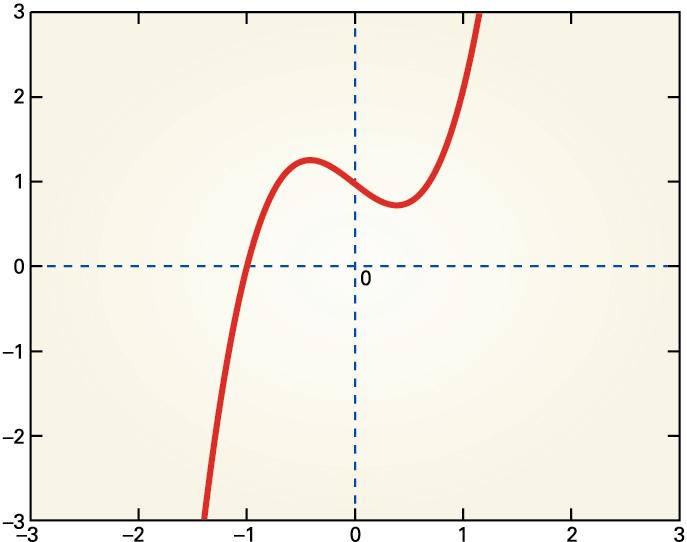
funtzio polinomiala
Matematikaren oinarrizko funtzioen artean,
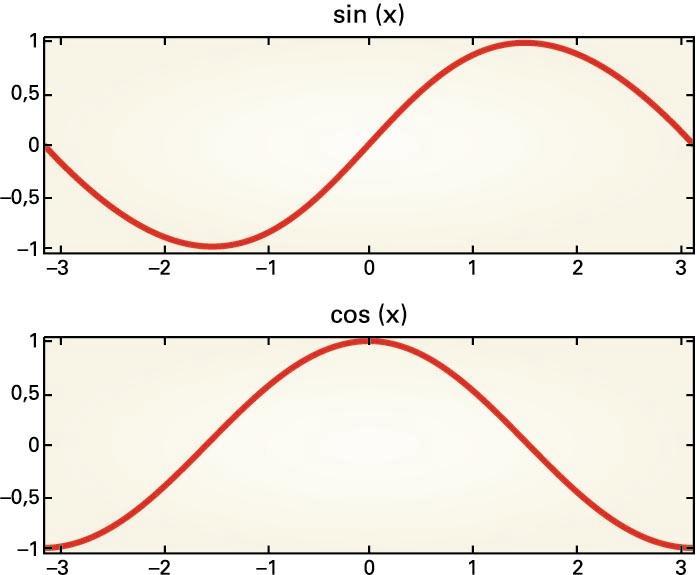
funtzio trigonometrikoak
ditugu,
adibidez, eta ,
sinu eta kosinu funtzioak, non
x
angelu baten neurri bat den. Funtzio trigonometrikoak
periodikoak direnez, naturan errepikatzen diren fenomenoak deskribatzeko
erabiltzen dira.
Grafiko hauek eta
funtziokoak dira:
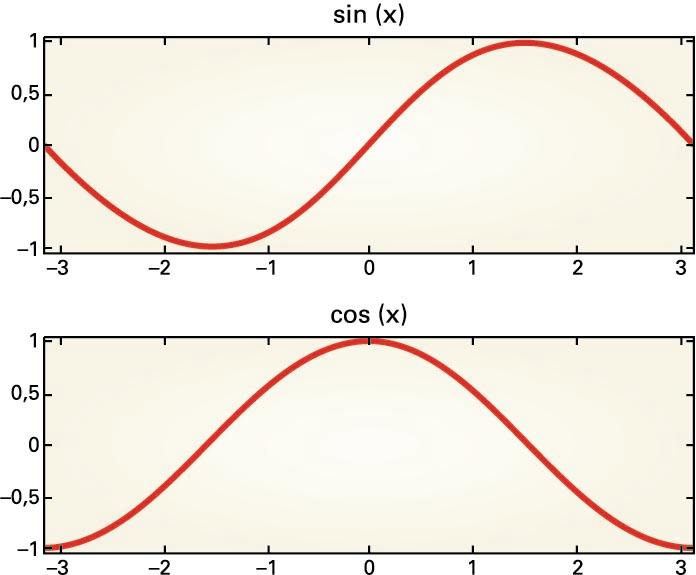
Funtzio trigonometrikoak: eta funtzioak
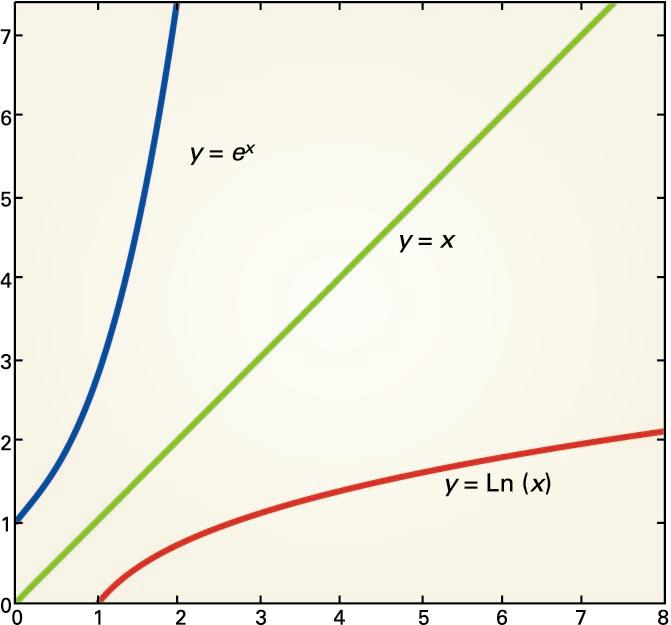
Funtzio esponentziala:
funtzioa da, non zenbaki positiboa eta edozein zenbaki erreal baitira. Funtzio
esponentzialen artean garrantzitsuena funtzioa da, non zenbakia (2,7182818…) logaritmoen sistemaren oinarria den.
Funtzioen arteko eragiketak
eta bi funtzio badira, eragiketa hauek definitzen
dira:
-
Batuketa:
,
,
konstantea eta funtzioa izanik.
-
Konposaketa: .
Adibidez,
eta
badira,
,
eta
.
Funtzio injektiboa
funtzioa injektiboa dela esango dugu, baldin
eta bi punturen irudiak desberdinak badira; hots, eta funtzioaren definizio-eremuko puntuak badira,
orduan,
Alderantzizko funtzioa
Izan bedi
funtzioa injektiboa. -ren alderantzizko funtzioa ikurraren bidez adierazten da, eta honela
definitzen da:
,
puntua funtzioaren irudi-multzoko puntua bada.
Funtzio esponentzialaren alderantzizko funtzioa
funtzio logaritmikoa da; funtzioaren alderantzizko funtzioa funtzioa da.
eta funtzioen grafikoak zuzenarekiko simetrikoak dira, grafiko
honetan ikus daitekeenez.
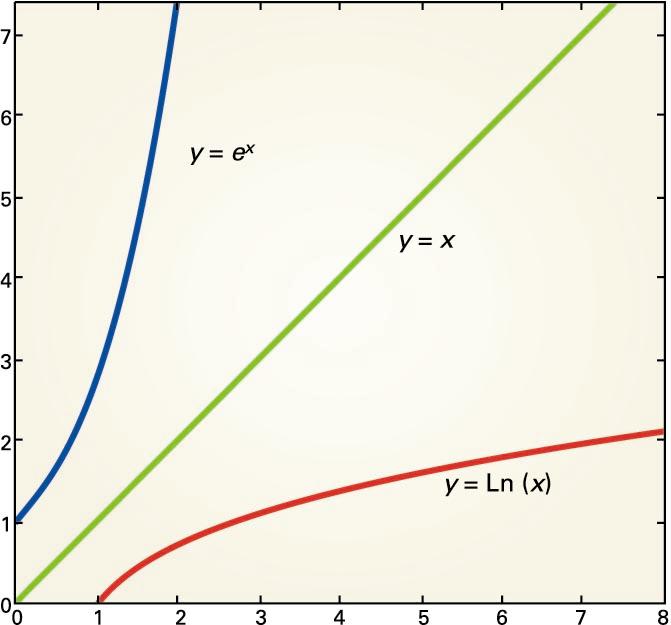
eta funtzioen grafikoak