electromagnetismo
- 1. Fis.
- Eremu elektriko eta eremu magnetikoen arteko eraginen ondoriozko fenomenoen multzoa.
Elektromagnetismoa Edit
Egilea: Jon Gutierrez
Elektromagnetismoa aldi berean fenomeno elektriko eta magnetikoak azaltzen dituen fisikaren arloa da. XIX. mendearen hasieran, elektrizitatea eta magnetismoa naturan behatutako karga elektriko eta iman iraunkorrei lotuta zeuden, hurrenez hurren. Fenomeno erabat ezberdinak zirela onartuta zegoen. Hori dela eta, elektromagnetismoaren garapen historikoa aurreko bi arloen historia da, hain zuzen ere.
Garapen historikoa
Antzinako greziarrek bazuten fenomeno elektrikoen (Tales Miletokoa, K.a. 624-546) eta magnetikoen (Tito Lukrezio, K.a. 99-55 eta Plinio Zaharra, 23-79) berri, eta fenomeno haien iturria gorputzek zuten barneko ‘arima’ zela uste zuten. Historian fenomeno horiei buruz agertzen den lehen argitalpena 1600. urtekoa da, William Gilbertek (1544-1603) idatziriko De Magnete liburukoa. Harrezkero, zientzialari asko saiatu ziren zientzia berri haien oinarri teoriko zein esperimentalak ipintzen, baina oinarri haiek ez ziren finkatu XVIII. mendearen amaiera arte.
Elektrostatika
Geldiunean dauden karga elektrikoen arteko elkarrekintza aztertzen du elektrostatikak. 1785. urtean, elkarrekintza horretarako lege ospetsu bat proposatu zuen Charles-Augustin Coulombek (1736-1806): geldiunean dauden bi karga puntualen arteko elkarrekintza (F indarra) karga-kantitateekiko proportzionala da, eta, distantzia, karratuarekiko alderantzizko proportzionala, sortutako indar erakarle (mota ezberdinetako kargak badira) edo indar aldaratzaile (mota bereko kargak badira) horren norabidea karga biek osotzen duten zuzenarena izanik.
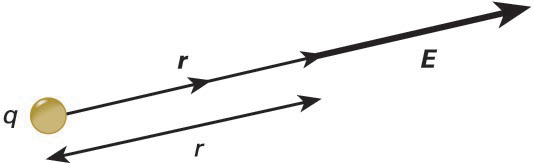
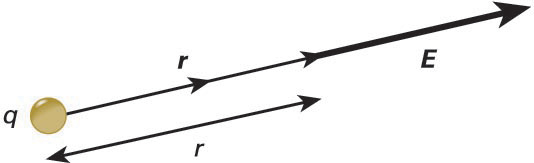
Argi dagoenez, karga batek bere inguruko espazioaren ezaugarriak aldatzen ditu, zonalde horretan beste karga bat kokatuz gero azken horrek indar bat jasango baitu. Hau da, karga elektriko batek E eremu elektrikoa sortzen du, eta puntu bateko eremu elektrikoaren intentsitatea (balioa) puntu horretan kokatuta legokeen karga batek jasango lukeen karga-unitateko indarra da: E = F / q’, non q’ karga indarra jasaten duena den. Zuzenean eman diezaiokegu eremu elektrikoari azalpen matematiko bat, Coulomben emaitzaz baliatuz:
non Ke konstante elektrikoa, q eremu elektrikoaren karga sortzailea eta r, berriz, q kargatik eremua kalkulatu nahi dugun punturaino neurtutako distantzia diren, hurrenez hurren.
Magnetostatika
1820ko uztailaren 21ean, Hans Cristian Oersted (1777-1851) hitzaldi bat ematen ari zela, iparrorratz baten gainean korronte elektrikoa zeraman hari eroale bat utzi, eta ustekabean orratza mugitu egin zen. Aspalditik eztabaidatzen zuten zientzialariek elektrizitatea eta magnetismoa erlazionatuta ote zeuden; hala ere, Oersted izan zen erlazioren bat eduki behar zutela esperimentalki frogatu zuen lehenengoa.
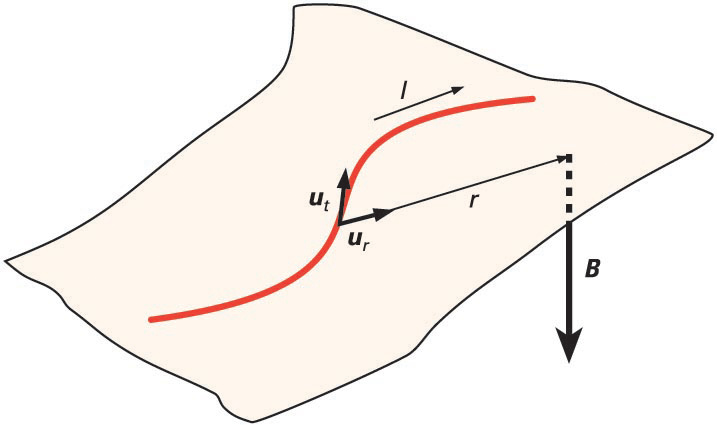
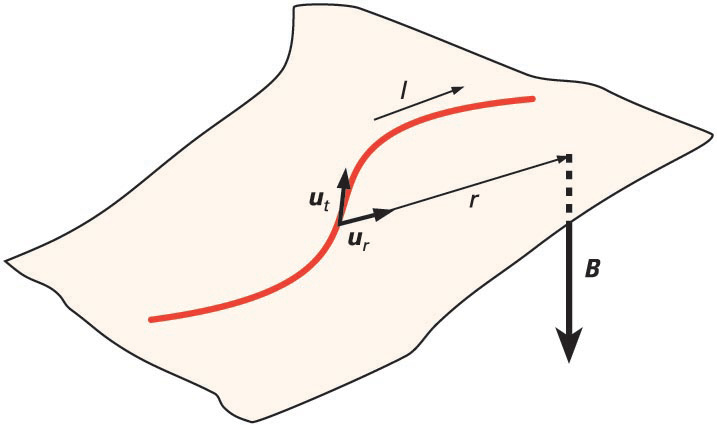
Handik aurrera, eta lehia azkar batean, lehenik André Marie Ampèrek (1775-1836), 1820ko irailaren 18an, korronte elektrikoen arteko jatorri magnetikodun indarrak aztertuz eta urte bereko urriaren 30ean Jean Baptiste Biot (1774-1862) eta Felix Savart (1791-1841) zientzialariek, bakoitzak bere bideari jarraituz, beren emaitzak aurkeztu zituzten I korronte elektriko egonkorrek sortutako B eremu magnetikoei buruz. Laburbilduz, hau dio Biot-Savart legeak:
non Km konstante magnetikoa, I eremu magnetikoaren korronte elektriko sortzailea eta r korronte hartatik kalkulatu nahi dugun punturaino neurtutako distantzia diren, hurrenez hurren. ut bektore unitarioak adierazten du korronte elektriko horren norabidea, eta ur-k, kalkuluari dagokion puntu horren posizio-bektorearen norabidea.
Elektrostatikaren eta magnetostatikaren oinarrizko legeak antzekoak dira: bietan konstante bat (Ke eta Km), elementu sortzaile bat (q eta I) eta distantziaren karratuaren alderantzizkoarekiko proportzionaltasuna agertzen dira. Baina, aldi berean, ezberdintasun handiak ere badaude, besteak beste sortutako eremuen norabideari buruzkoak: elkarrekintza elektrikoaren norabidea karga sortzaileak eta espazioko puntu batek osotzen duten lerro zuzenarena bada ere, elkarrekintza magnetikoa beti agertuko da korronte elektriko sortzaileak eta espazioko puntu horrek osoturiko planoarekiko norabide perpendikularrean, ut × ur biderkadura bektorialak adierazten duen moduan.
Elektrodinamika
Hala ere, aurreko adierazpen biek daukate elementu komun nabari bat: eremu elektrikoaren iturria q karga elektrikoa da, eta eremu magnetikoaren iturria, berriz, I = dq / dt da, hots, mugitzen den karga elektrikoa! Garai hartako zientzialariek egin zuten galdera zuzena hau zen: fenomeno elektriko eta magnetikoen iturria beti karga elektrikoa bada, ez ote da posible eremu bakar batekin ari garela pentsatzea?
Zientzialari haien artean, A. M. Ampère izan zen lan horri gogor ekin zion lehenengoa; aipatu dugunez, bereziki korronte elektrikoek daramaten hari eroaleen arteko indarrak aztertu zituen. Ampèrek 1826ko azaroan argitaratu zituen bere ikerketaren emaitzak. Baina Oerstedek egindako asmakuntzatik hamaika urtera, 1831. urtean, Michael Faradayk (1791-1867) frogatu zuen eremu magnetiko aldakor batek sor dezakeela (induzitutako) eremu elektriko bat. Beste hitz batzuetan esanda, Faradayk frogatu zuen fluxu magnetiko aldakor baten barnean mugitzen ari den edozein eroalek sorgailu elektriko gisa joka dezakeela.
Orduan, landuta geratu ziren zientzia berri haren zutabeak: eremu elektriko batek sor dezake eremu magnetiko bat (Oersteden saiakuntza) eta eremu magnetiko batek sor dezake eremu elektriko bat (Faradayren saiakuntza). Baina zertan datza eremu klasiko horien ikuspegi berri hau?
Maxwellen ekuazioak
James Clark Maxwell (1831-1879) jeinu bat zen, eta XXI. mendean ere maila berean kokatu behar ditugu haren azkartasuna eta Newtonena eta Einsteinena. Besteak beste, distantziarako elkarrekintzak, gasak, koloreak, eta bereziki elektrizitatea eta magnetismoa izan ziren haren ikerketaren gai nagusiak.
1865etik 1871ra bitartean idatzi zuen Maxwellek bere lan famatuena: A Treatise on Electricity and Magnetism. Liburu hartan, aurretik asmatutako elektrizitatea eta magnetismoari buruzko lege guztiei esangura fisiko bakarra eman zien Maxwellek: eremu elektromagnetikoarena.
Lege horiek multzo batean biltzen dira, Maxwellen ekuazioak deritzon multzoan, hain zuzen ere, eta eremuak hutsean daudela kontsideratuz gero:
| (1) |
| (2) |
| (3) |
| (4) |
non ρ eta J karga elektrikoaren eta korronte elektrikoaren dentsitate-sortzaileak diren, hurrenez hurren, eta ε0 hutsaren permitibitate elektrikoa eta μ0 hutsaren iragazkortasun magnetikoa diren. Aurreko lau ekuazioek osotzen dute elektromagnetismo klasikoa izeneko fisikaren arloa, beste kontzeptu hauekin batera: ingurune (eroale, dielektriko edo magnetiko) bakoitzaren ezaugarriak, eta Lorentzen indarra: , non q karga puntual batek jasaten duen indar netoa den aldi berean eremu elektriko eta magnetiko baten pean mugitzen denean.
Maxwellen lau ekuazio horiei interpretazio egoki bat eman diezaiegun, kontuan hartu beharko dugu dibergentzia (div) izeneko eragiketa matematikoa eremu baten iturriekin zuzenean erlazionatuta dagoela. Bestalde, errotazionala (rot) eragiketak adieraziko digu nolakoa den dagokion eremua lerro itxi baten gainean neurtuta. Hori dela eta, lehenengo ekuazioa Faradayren indukzio elektromagnetikoaren legea dugu; lege horrek esaten du eremu magnetiko aldakor batek eremu elektriko bat sor dezakeela. Bigarrena Gaussen legea dugu elektrizitatean (hots, karga elektrikoa dela eremu elektrikoaren iturria), eta Coulomben legearen baliokidea dugu. Hirugarren legea Ampèreren emaitza famatuena eta Maxwellek egindako zuzenketa da; lege horrek dio eremu magnetikoaren iturri bakarra ez dela korronte elektrikoa, eta eremu elektriko aldakorra ere badela iturria. Eta, bukatzeko, (4). ekuazioak esaten du eremu magnetikoak ez duela karga (polo) magnetiko sortzaile isolaturik; polo magnetikoak beti agertuko dira bikoteka, ipar-poloa dagokion hego-poloarekin. Azken lege hori Biot eta Savarten legearen ondorio zuzena da.
Baina Maxwellen ekuazioak sakon aztertuz gero, oraindik gehiago ondoriozta daiteke: eremu magnetiko aldakor batek eremu elektriko bat sortzen badu (aldakorra, (1). ekuazioa) eta eremu elektriko aldakor batek eremu magnetiko bat sortzen badu (aldakorra, (3). ekuazioa), erlazio horiek esaten digute aldi berean eremu biak (elektrikoa eta magnetikoa) izaten direla, eta eremu bakarra osotzen dutela, eremu elektromagnetikoa , hain zuzen ere. Eremu elektromagnetiko bakarra dugu egoera orokorrenean, hau da, bi osagaiak, eremu elektrikoa eta magnetikoa, denborarekin aldakorrak direnean [E(t) eta B(t) direnean]. Arrazonamendu horrekin jarraituz, elektrostatika eta magnetostatika elektromagnetismoaren bi azpiarlo bihurtuko lirateke, denborarekiko aldaketa horien maiztasunak zerorantz jotzen dutenean (edo, gutxienez, oso txikiak direnean).
Uhin elektromagnetikoak
Maxwellek ateratako ondorioetako bat oso garrantzitsua da: iturririk ez badago ere (ρ = J = 0), behin eremu elektromagnetikoa sortuta dagoenean, espazio osora hedatuko da uhin baten moduan, eta uhin elektromagnetikoak osotuko ditu. Maxwellek kalkulatu zuen hutsean bidaiatzen duen uhin elektromagnetiko baten hedapen-abiadurak honelakoa izan beharko zuela:
1856. urtean, Leipzigen Wilhelm Weber (1804-1891) eta Rudolph Kohlrausch (1809-1858) zientzialariek eginiko ε0 eta μ0 magnitudeen neurketez baliatuz, Maxwellek finkatu egin zuen v hori: 2,9979 × 108 m/s-ko balioa lortu zuen. Balio hori eta 1849. urtean Armand H.L. Fizeauk (1819-1896) lortutako argiaren abiadura (3,153 × 108 m/s) hain antzekoak zirenez, Maxwellek proposatu zuen argia ere uhin elektromagnetiko bat dela.
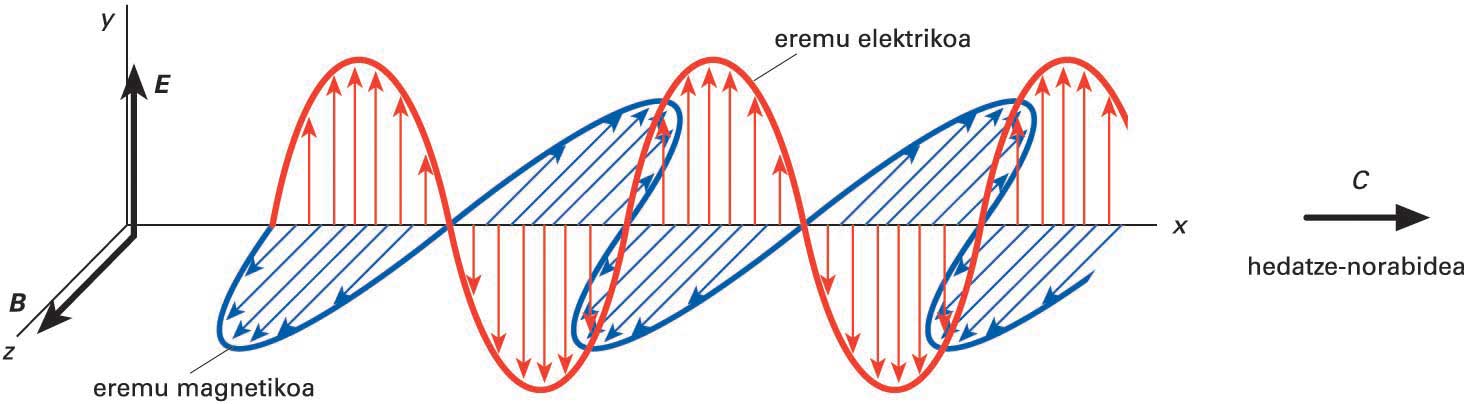
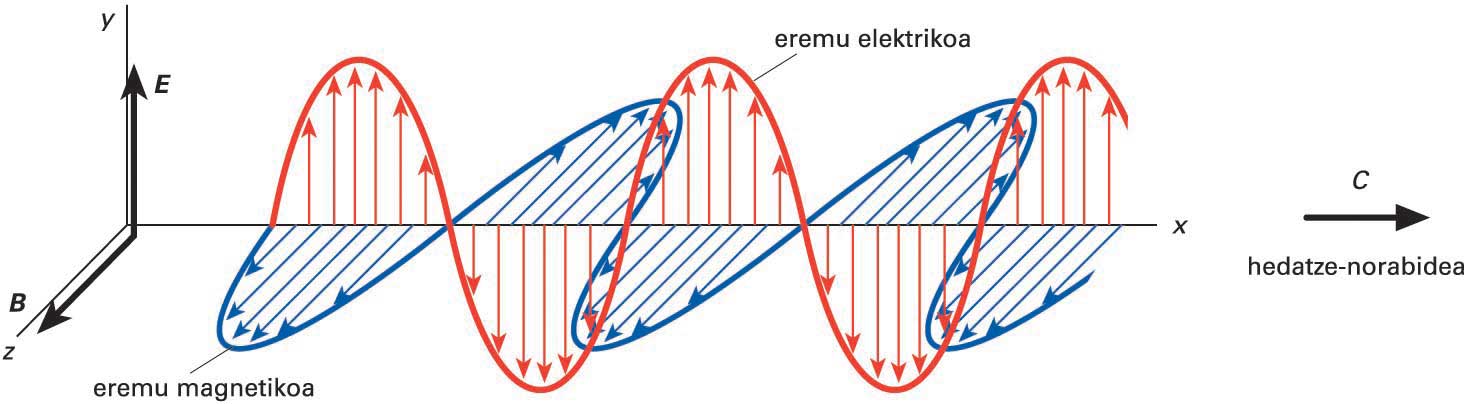
Uhin elektromagnetiko baten itxura
Baina abiadura hori (hutsean), c, ez da uhin elektromagnetiko batek duen ezaugarri bakarra. E eta B bektore elektrikoa eta magnetikoa elkarrekiko perpendikularrak izango dira, eta, aldi berean, biak hedapen-norabidearekiko perpendikularrak; eta, azkenean, bi eremu horiek erlazio honen bidez erlazionatuta egongo dira: E / B = c. Ezaugarri horiek beteko dira hedapenaren edozein puntu eta unetan.
Hala ere, Maxwellek eginiko lana, hots, eremu elektromagnetikoaren interpretazioa eta argiaren izaera elektromagnetikoarena, guztiz teorikoa zen. Heinrich R. Hertzek (1857-1894) frogatu zuen, 1888. urtean, uhin elektromagnetikoak beste edozein motatako uhinak bezalaxe sortzen eta hedatzen direla. Are gehiago: bere emanaldian, Hertzek uhin elektromagnetikoen errefrakzioa, islapena, difrakzioa eta polarizazioa erakutsi zituen, eta, hala, uhin elektromagnetikoek argiaren ezaugarri berdinak zituztela frogatu zuen. Hots, Hertzek esperimentalki erakutsi zuen argia beste uhin elektromagnetiko bat izan zitekeela.
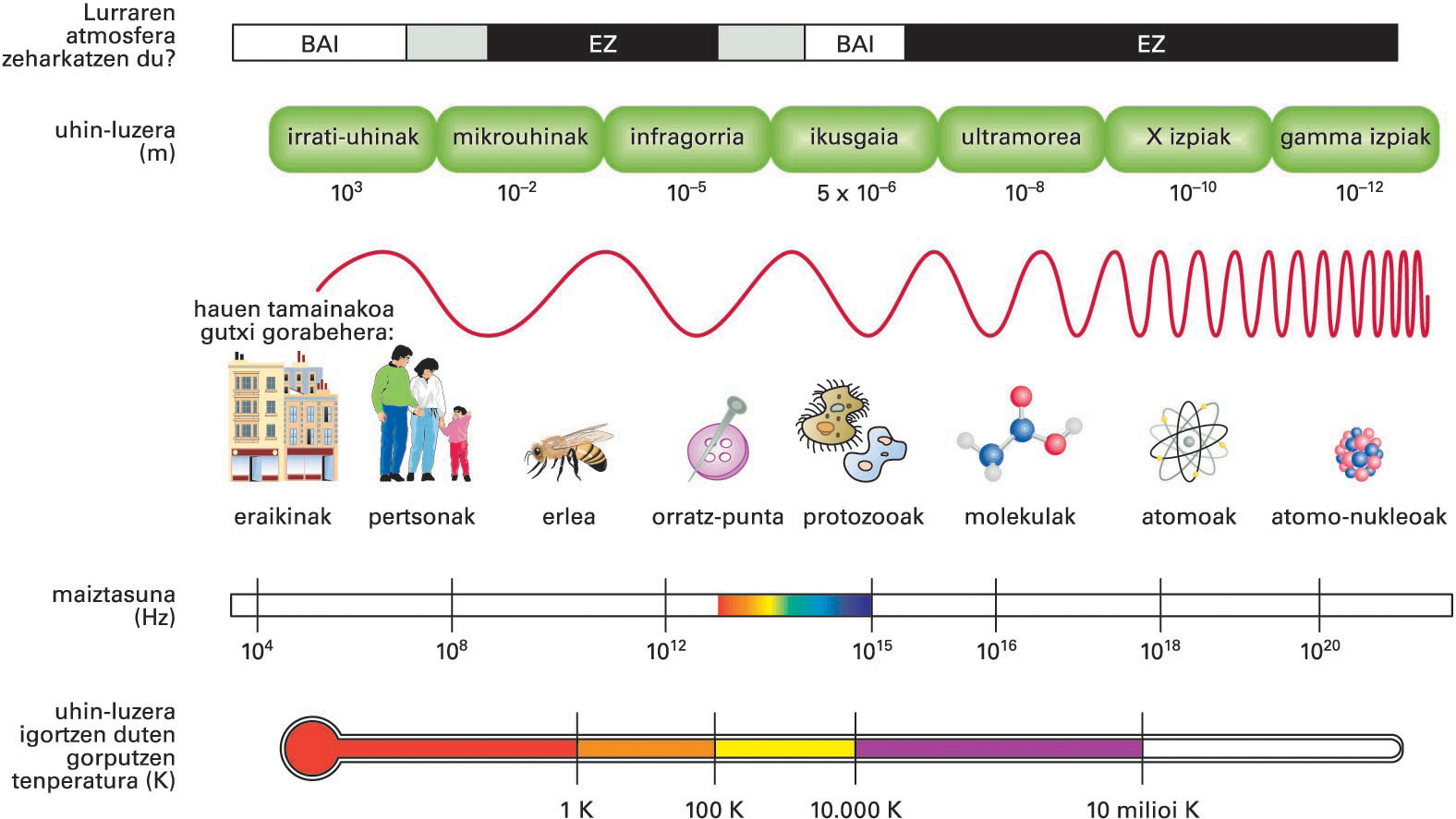
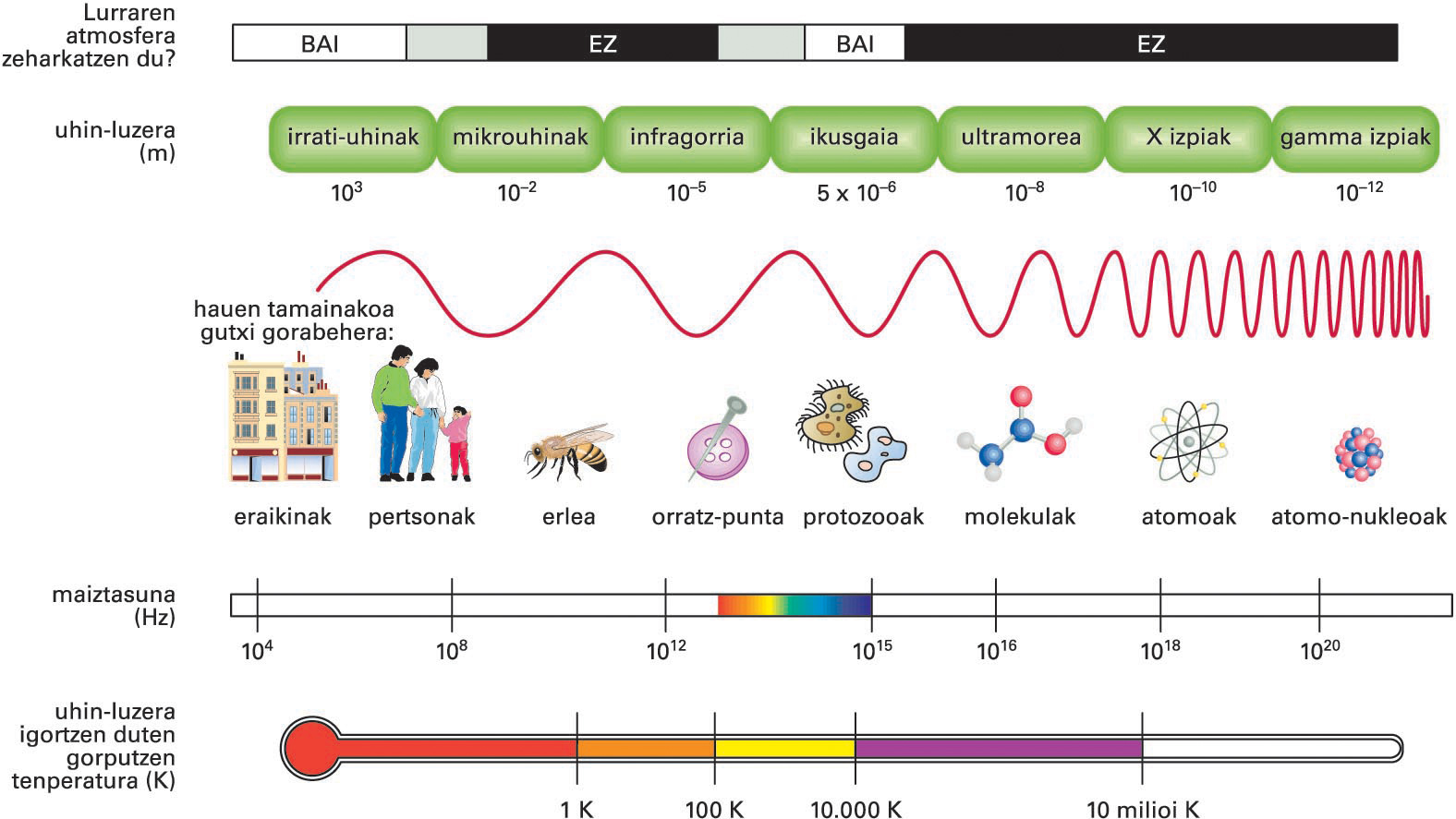
Uhin elektromagnetiko mota asko daude, bakoitza bere uhin-luzerarekin, maiztasunarekin edo energia bereizgarriarekin (hiru magnitude horiek zuzenean erlazionatuta baitaude); uhin elektromagnetiko guztien multzoari espektro elektromagnetiko deritzo, uhin-luzera edo maiztasunaren arabera sailkaturik. Hori dela eta, maiztasuna handituz, izango ditugu (109 Hz-eraino), mikrouhinak (3 × 1011 Hz-eraino), uhin infragorriak (4 × 1014 Hz-eraino), argi ikusgaia (4-8 × 1014 Hz-eraino), izpi ultramoreak (3 × 1017 Hz-eraino), X izpiak (3 × 1017-5 × 1019 Hz-eraino), γ izpiak (3 × 1018-3 × 1022 Hz-eraino), eta izpi kosmikoak. Nabarmentzekoa da argi ikusgaiari (begiak ikus dezakeen uhin elektromagnetikoen multzoari) dagokion tarte estua; tarte horren barnean daude kolore guztiak.
Espektro elektromagnetikoa
Maxwellen ekuazioak eta horien ondorioak benetako iraultza izan ziren garai hartako zientzia-komunitatean. Maxwell hil zen urte berean jaio zen Albert Einstein (1879-1955) zientzialari ospetsua. Einsteinek, Maxwellek azaldutako elektromagnetismoaren legeek erreferentzia-sistema inertzial guztietan baliokideak izan behar zutela ikusita, 1905. urtean argitaratu zituen erlatibitate bereziaren oinarrizko printzipioak (fisikaren lege guztiak era berean agertzen direla eta c hutseango argiaren abiadura konstante dela, erreferentzia-sistema inertzial guztietan).
Aplikazioak
Elektromagnetismoaren aplikazioak, eta bereziki uhin elektromagnetikoenak, gure eguneroko bizimoduaren arlo askotan aurki ditzakegu. Gure etxeetan ere, indukziozko sukaldea eta mikrouhin-labe bat dauzkagu ia guztiok, seguru. Are gehiago: etxean erabilitako tentsio elektriko alternoa indukzio elektromagnetikoan oinarritutako sorgailu elektriko bat erabiltzen delako eskuratzen dugu; sorgailu berezi horri alternadore deritzo.
Industrian, berriz, asmakuntza garrantzitsuenetako bat elektroimana izan zen. Elektroiman baten hariletik korronte elektrikoa pasatzean, barnean dagoen burdinazko nukleoaren ezaugarri magnetikoa handiagotzen da. Propietate hori dela eta, txirrin elektrikoen, kontaktoreen, voltmetro eta amperemetroen eta, bereziki, motor elektrikoen funtsezko atala dira elektroimanak.
Hainbat zientzia-arlotan erabiltzen dira izpi ultramoreak (fisikan eta kimikan), X izpiak (medikuntzan eta fisikan) eta γ izpiak (fisika nuklearrean). Eta, zer esanik ez, gaur egun, komunikazioen garaian bizi gara, eta lortu dugun informazioaren hedatze-abiadura azkarra ezinezkoa litzateke uhin elektromagnetikoak erabili gabe. Adibide gisa, irrati eta telebistaren uhinak, sateliteek erabilitako seinaleak, eta 1990eko hamarkadan telefono mugikorrek telekomunikazioen arloan eragindako aldaketak aipa ditzakegu; horiek guztiak uhin elektromagnetikoaz baliatuz.