Matematikan, deribatuaren kontzeptua kalkulu
infinitesimalaren oinarrizko kontzeptua da. Funtzioaren hazkundea
aldagaiarekiko aztertzen da deribatua erabiliz. eta bi magnitudeen arteko erlazioa
funtzioaren bidez adierazten bada,
aldagai independentearen aldaketak eginez
sorturiko -ren aldaketak neurtzen dira funtzioaren
deribatua erabiliz. Deribatuaren bidez, aldaketa-koefizientearen kontzeptua
ezartzen da zientzia-arlo guztietan, eta deribatua funtzioaren aldaketaren
oinarrizko adierazle bihurtzen da. Deribatua definitzeko, bi hurbilketa erabil
daitezke: bata, fisikakoa eta, bestea, geometrikoa.
Deribatuaren kontzeptua fisikan
Newtonek abiaduraren kontzeptua erabili zuen
mekanikako oinarriak ezarri zituenean. Demagun A puntutik B puntura mugitzen
garela, zein izango da batez besteko abiadura? Alde batetik, A eta B-ren
arteko distantzia eta; beste aldetik, erabilitako denbora kalkulatzen ditugu.
Bi magnitude horien zatiketa batez besteko abiadura izango da. Orain, demagun A
eta B puntuak oso hurbil daudela; erabili beharko dugun denbora ere oso txikia
izango da. Suposa dezagun
denboran A puntuan gaudela, eta
denboran, B puntuan; A eta B-ren arteko
distantzia
bada,
batez besteko abiadura =
izango da.
gero eta txikiago egiterakoan, beraz,
limitera pasatzerakoan, A puntuko aldiuneko abiadura definitzen da:
aldiuneko abiadura (A puntuan) = .
Posizioa
denboran
bada, orduan,
aldiuneko abiadura (A puntuan) =
.
Abiaduraren kontzeptua orokortzen da edozein
menpeko aldagairen aldaketa-koefizientea aldagai independentearekiko
kalkulatzeko.
Geometrikoki, aldagai errealeko funtzioa bada eta funtzio horren grafikoa ( puntuen multzoa, non puntua funtzioaren definizio-eremuko puntua, kontsidera dezagun grafikoko puntu bat . Puntu horretan grafikoa nahiko “leuna” bada, kurba bakarrik puntu horretan
ukitzen duen zuzen bat marraz daiteke. Zuzen hori kurbarekiko puntu horretako
zuzen ukitzailea izango da. Zuzen ukitzailearen malda kalkulatzeko, kurbako
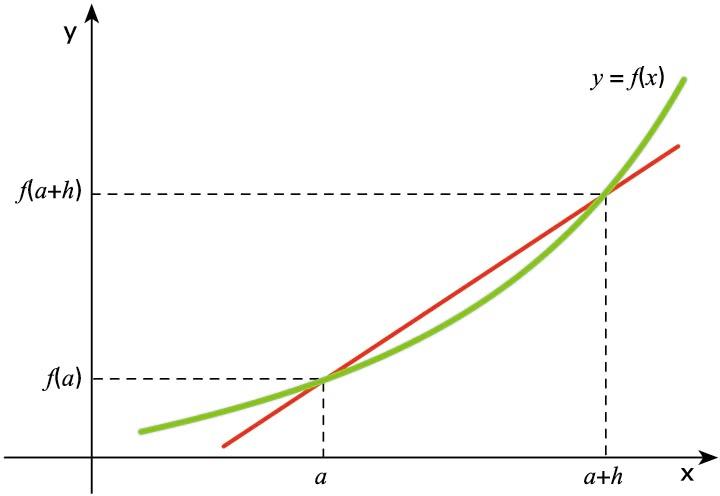
beste puntu bat kontsideratzen dugu. Bi puntu horietatik
pasatzen den zuzen ebakitzailearen malda hau da:
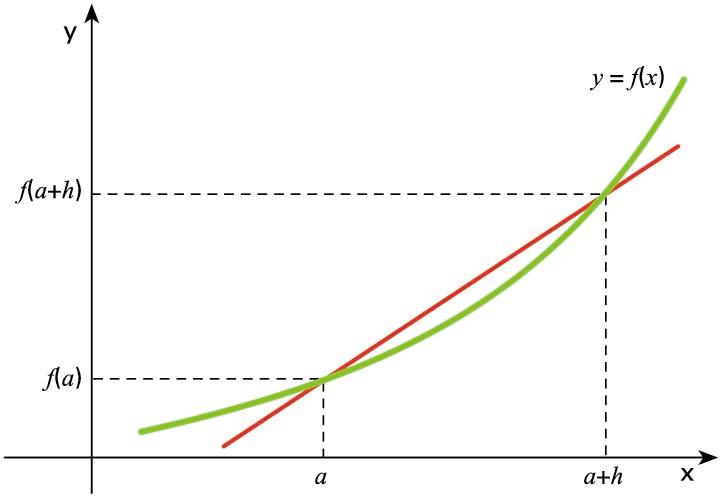
kurbaren zuzen ebakitzailea
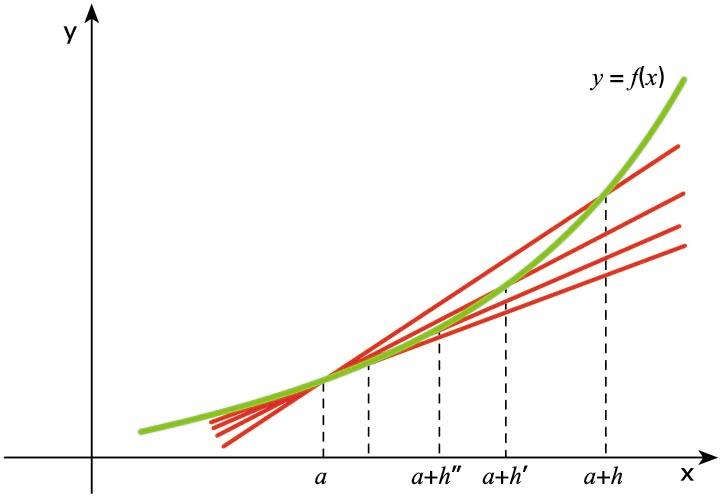
puntua -rantz hurbildu ahala, zuzen ebakitzailea
zuzen ukitzaile bihurtuko da.
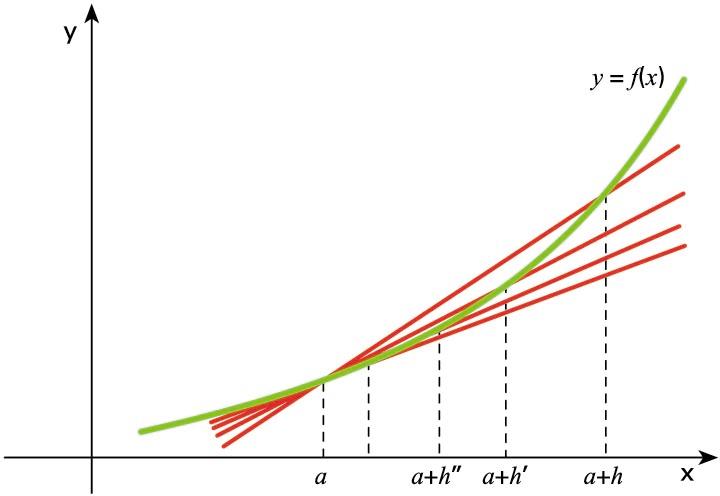
h
desberdineko zuzen ebakitzaileak
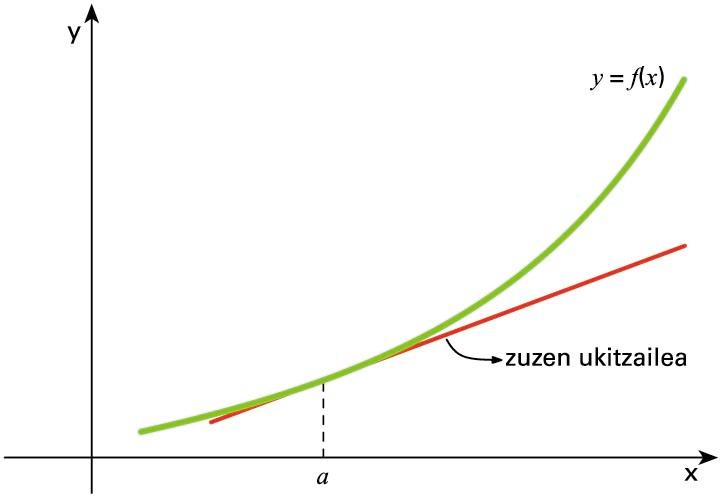
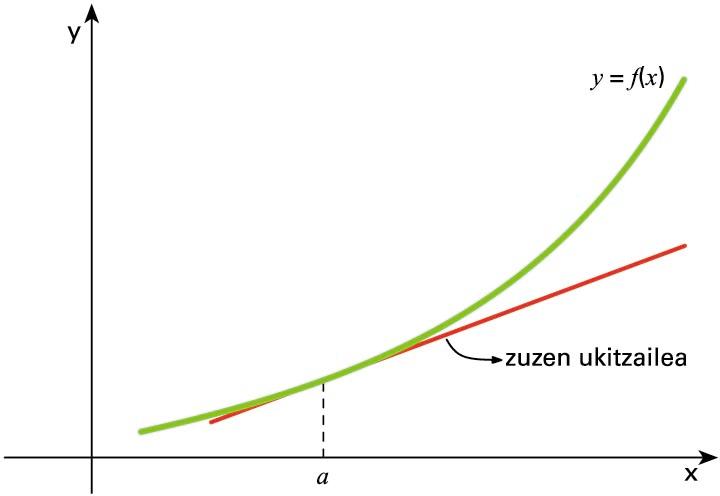
Zuzen ukitzailea
Hori dela eta,
puntuko zuzen ukitzailearen malda limite
baten bidez adieraz daiteke:
Deribatuaren definizioa
Esango dugu funtzioa deribagarria dela puntuan, baldin eta aurreko limitea
existitzen bada, eta limitearen balioa funtzioaren deribatua izango da puntuan. Lagrangeren notazioan funtzioaren deribatua adierazteko
ikurra erabiltzen da. Honela:
.
Beraz, funtzioaren deribatua puntuan kurbarekiko zuzen ukitzailearen malda izango
da; grafiko batean, maldak funtzioaren hazkundea adierazten du.
Deribagarritasuna eta jarraitutasuna
funtzioa deribagarria bada puntuan, orduan, jarraitua da puntu horretan.
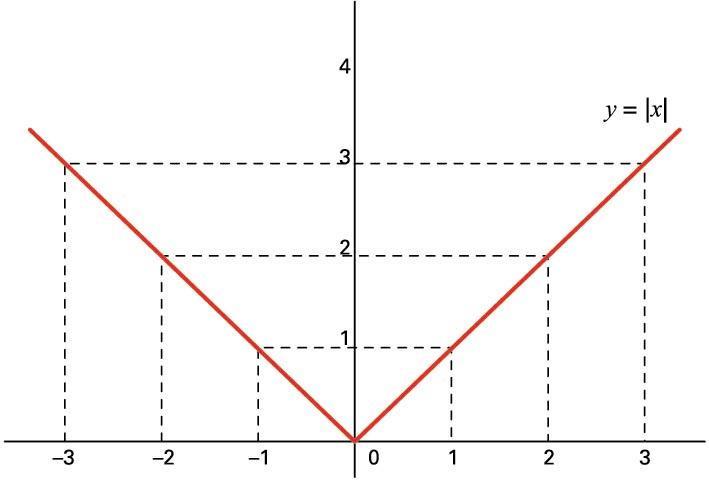
Baina ez alderantziz: funtzioa jarraitua da puntuan, baina ez deribagarria. positiboa bada, zuzen ebakitzailearen malda (-tik -ra) da, baina negatiboa denean, .
funtzioak puntuan ertz bat du, grafiko honetan ikus
daitekeenez:
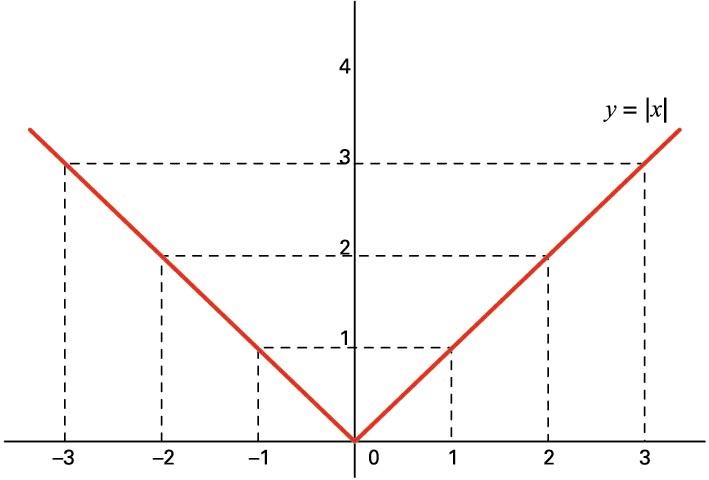
funtzioaren grafikoa
funtzioa deribagarria bada D eremuko puntu
guztietan, esango dugu deribagarria dela D eremuan. Kasu horretan, D eremuan funtzioaren deribatua definitzen da.
Kontsidera dezagun, adibidez, funtzioa, orduan,
Lagrangeren notazioa
:
funtzioaren deribatua.
:
funtzioaren bigarren deribatua.
:
funtzioaren hirugarren deribatua.
:
funtzioaren -garren deribatua.
Leibnizen notazioa
funtzioaren deribatua adierazteko, notazio
hau ere erabiltzen da:
eta -garren deribatua
Leibnizen notazioan adierazten da deribatua zein
aldagairekiko kalkulatzen den. Funtzioa bi aldagaikoa edo gehiagokoa bada,
deribatua aldagai bakoitzarekiko deribatu partziala izango da. Adibidez,
bi aldagaiko funtzioa baldin bada,
funtzioaren deribatua aldagaiarekiko
izango da, eta -garren deribatu partziala -rekiko.
Funtzio elementalen deribatuak
Funtzio elementalen deribatuak limitearen
definizioa erabiliz kalkulatzen dira; hauek dira:

Deribatuaren propietateak
1.
eta funtzioak deribagarriak badira puntuan, orduan, funtzioa ere deribagarria da puntu horretan,
eta
2. eta funtzioak deribagarriak badira puntuan, orduan, funtzioa ere deribagarria da puntu horretan,
eta
3. funtzioa deribagarria bada puntuan eta ,
orduan, funtzioa deribagarria da puntuan, eta
4. Katearen erregela. Baldin eta
funtzioa puntuan eta funtzioa
puntuan deribagarriak badira, orduan, deribagarria da puntuan, eta
Gorakortasuna eta beherakortasuna
Funtzioa deribagarria denean, deribatua
aztertuz zehazten da funtzioaren gorakortasuna eta beherakortasuna. Kontsidera
dezagun tartean jarraitua eta -n deribagarria den funtzioa, orduan,
-
bada tartean, orduan, funtzioa gorakorra da tartean.
-
bada tartean, orduan, funtzioa beherakorra da tartean.
-
bada tartean, orduan, funtzioa konstantea da tartean.