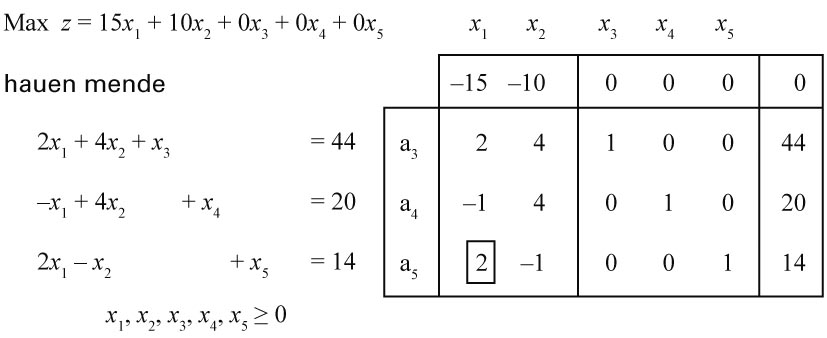George B. Dantzigek argitaratu zuen 1949. urtean, eta eredu lineal honen moduko ereduen soluzio optimoa kalkulatzeko balio du:

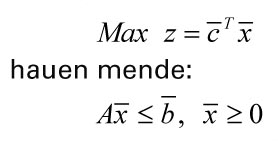
(1)

$z={\overline{c}}^T\overline{x}$ helburu-funtzioaren balio maximoa aurkitu nahi da. Betiere $\overline{x}$  bektoreko aldagaiek inekuazio-sistema beteko dute, eta ez-negatibo izango dira.

Metodoa adibide baten bidez uler daiteke. Hasteko, ebazpen grafikoa erakutsiko da, grafikoak modu intuitiboan erakusten baititu eredu linealaren ezaugarriak eta ebazpenerako metodo aljebraikoa. Adibideko ereduko inekuazioek definitutako soluzioen multzoa kalkulatzeko, ekuazioak marrazten dira, eta gezien bidez adierazten da inekuazioek determinatutako erdiespazioa zein den. Horrela, beheragoko irudian ikusten den erpin-kopuru finituko poligonoa lortzen da, O, A, B, C eta D puntuek mugatutakoa.

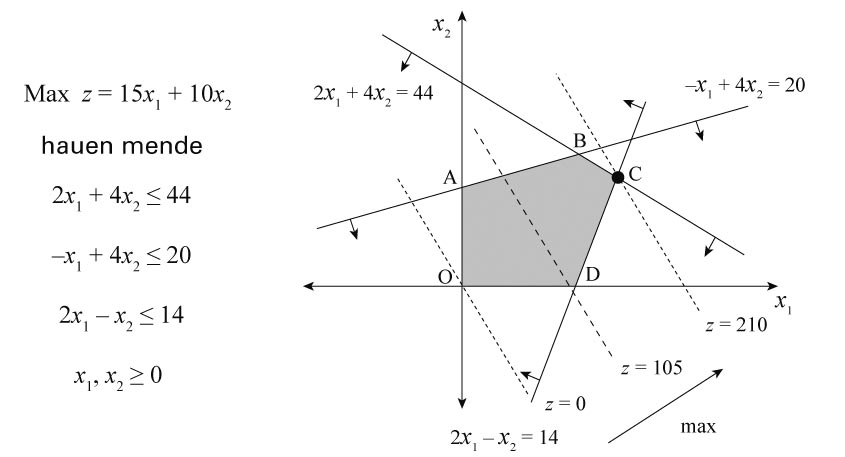
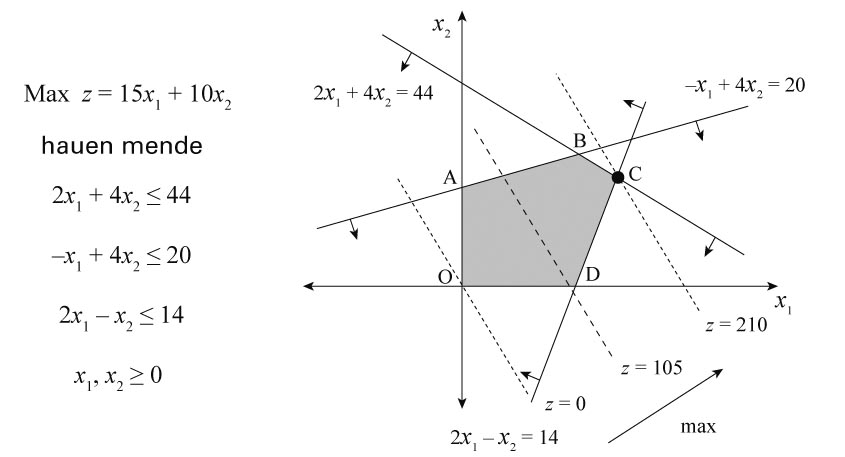
Eredu lineala eta ebazpen grafikoa

Helburu-funtzioa zuzen paraleloen familia bat da; $z$-ren balio bakoitzerako zuzen bat. Zuzena jatorri-puntutik aldenduz soluzioen multzoaren gainean desplazatzen den heinean, $z$-ren balioa hazi egiten da, eta balio optimoa multzoaren mugara iristean lortzen da. Helburu-funtzioaren balio optimoa beti erpin batean aurkitzen da, kasu honetan, C puntuan.

Ebazpen geometrikoaren erabilera bi edo hiru aldagai dituzten ereduetara mugatuta dago. Tamaina handiagoko ereduen ebazpenerako, beharrezkoa gertatzen da metodo aljebraiko bat erabiltzea: simplex algoritmoa. Metodoa erabili ahal izateko, (1) sistemako inekuazioak ekuazio bihurtu behar dira, nasaitze-aldagai izena duten ${\overline{x}}_s$ aldagaiak gehituz. Horrela lortzen da eredu transformatua.

,

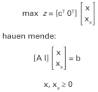(2)

Ekuazio-sistema bateraezina izan daiteke; baina, bateragarria bada, indeterminatua da. $m$ izanik linealki independente diren ekuazio-kopurua eta $n$ ezezagun-kopurua, sistemarako edozein soluziok $m$ oinarriko ezezagun eta $n-m$ aske ditu. Oinarriko ezezagun-multzo bat aukeratzen da, eta aske guztiei $0$ balioa emanez oinarriko soluzio izeneko soluzioa lortzen da. (2) eredukoaren moduko ekuazio linealetako sistema batek oinarriko soluzio-kopuru finitua du, eta oinarriko soluzio horiek bana-banako korrespondentzia dute (1) ereduko inekuazioek definitutako soluzioen multzoko erpinekin. Grafikoki ikusten da (1) ereduaren moduko soluzio optimoa soluzioen multzoaren erpin batean aurkitzen dela. Erpinen eta oinarriko soluzioen artean dagoen bana-banako korrespondentzia jakinda, esan dezakegu (2) motako ereduaren soluzio optimoa oinarriko soluzio batean aurkitzen dela.

Simplex algoritmoa metodo iteratiboa da. Oinarriko soluzio batetik abiatuz, hobea den beste oinarriko soluzio bat kalkulatzen da optimora iritsi arte. Kalkuluak egiteko, simplex taula erabiltzen da (ikus hurrengo irudia). $\left[A I\right]$matrizean, B oinarri bat aukeratzen da, eta ${\overline{x}}_B$ oinarriko soluzioa kalkulatzen da, baita $\left[A I\right]$matrizeko bektoreen koordenatuak B oinarrian ere, taulako $B^{-1}A$ eta $B^{-1}I$  elementuak, alegia. ${\overline{c}}_B$ bektoreak oinarriari dagozkion $\left[\overline{c} 0\right]$bektorearen osagaiak ditu, eta taulako goiko lerroa eta helburu-funtzioaren $z={\overline{c}}_B^T{\overline{x}}_B$ balioa kalkulatzeko erabiltzen da. Soluzioa ez da optimoa izango taulako goiko lerroan elementu negatiboak dauden bitartean.

Simplex taula

Hurrengo irudian, adibideko ereduari dagokion eredu transformatua ikus daiteke. Sistema transformatuaren matrizeko azken hiru zutabeek osatutako $B=\left\{{\text{a}}_3,{\text{a}}_4,{\text{a}}_5\right\}$ oinarria aukeratuta, dagokion simplex taula lortzen da (ikus hurrengo irudia).

Adibideko eredu transformatua eta simplex taula

Taulako oinarriko soluzioa (oinarriko aldagaiak: $x_3=\mathrm{44,}{x}_4=\mathrm{20,}{x}_5=14$ ; aldagai askeak: $x_1=\mathrm{0,}{x}_2=0$) 1. irudiko grafikoko $0$ erpinari dagokio. Baina, ez da optimoa simplex taulako goiko lerroan balio negatiboak daudelako.

Soluzioa hobetzeko, oinarritik aterako den bektore bat aukeratzen da, eta bere lekuan sartuko den beste bat ere bai. Oinarrian sartuko da taulako goiko lerroan balio negatiboen artean minimoari dagokion bektorea $(\min \left\{-\mathrm{15,}-10\right\}=-15);$ kasu honetan, ${\text{a}}_1$. Dagokion zutabeak pibot zutabea izena du. Oinarritik aterako den bektorea aukeratzeko, soluzioaren zutabeko osagaiak positibo diren pibot zutabeko osagaiekin zatitzen dira, osagaiz osagai. Horien artean minimoa aukeratuz, pibot errenkada finkatzen da. Aldi berean pibot zutabean eta pibot errenkadan dagoen taulako elementuari pibota esaten zaio. Adibiderako, $\min \left\{44/2,14/2\right\}=14/2$, beraz 3. errenkada da pibot errenkada, eta ${\text{a}}_5$ bektorea da oinarritik aterako dena.

Taula berria kalkulatzeko, errenkaden artean oinarrizko eragiketak egiten dira. Pibot errenkadako elementuak pibotaz zatitzen dira taula berriko 3. errenkada lortzeko (ikus hurrengo irudia). Gainontzeko errenkadei biderkatzaile batez biderkatua izan den pibot errenkada kenduko zaio. Biderkatzailea kalkulatzeko, aldi berean pibot zutabean eta eguneratu nahi den errenkadan dagoen elementua pibotaz zatituko da, $2/2$  eta $-1/2$, hurrenez hurren. Taulako goiko lerroa modu berean kalkulatzen da. 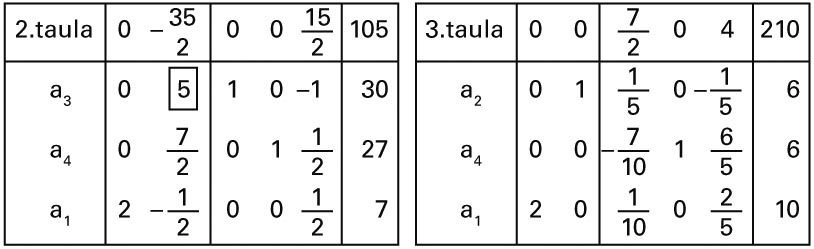Horrela lortzen da 2. simplex taula (ikus hurrengo irudia). Taula horretako oinarriko soluzioa (oinarriko aldagaiak: $x_3=\mathrm{30,}{x}_4=\mathrm{27,}{x}_1=7$; aldagai askeak: $x_2=\mathrm{0,}{x}_5=0$) 1. irudiko poligonoko D erpinari dagokio.

Prozedura bera errepikatzen da 3. simplex taula kalkulatzeko. Taula hori optimoa da goiko lerroan balio negatiborik ez duelako. Taula horretako oinarriko soluzioa poligonoko C erpinari dagokio.

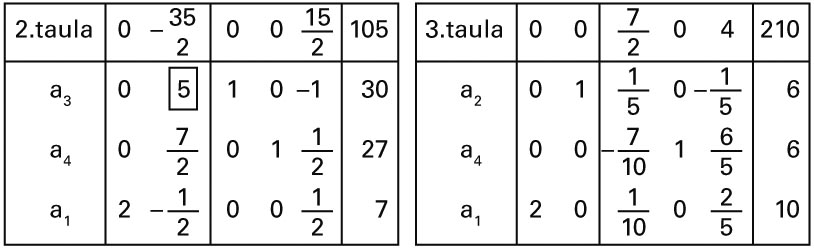
2. eta 3. simplex taulak

Ereduaren murrizketak (1) eredukoarenak bezalakoak ez diren kasurako, hau da $\ge$ modukoak direnean, eredu transformatua lortzeko nasaitze-aldagaiak kendu egin behar dira. Eta, helburua minimizatzea denean, helburua transformatu egiten da maximizatze-idazkerara egokitzeko.
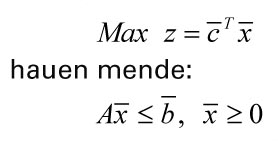
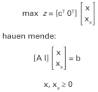